DATA Camp M2

Partie 1 : Analyse de données

Rappels Fondamentaux

Qu’est ce qu’une variable ?

Une variable statistique est une caractéristique ou une mesure que l’on peut attribuer à chaque individu d’une population ou d’un échantillon.

Tableau du type de variable :

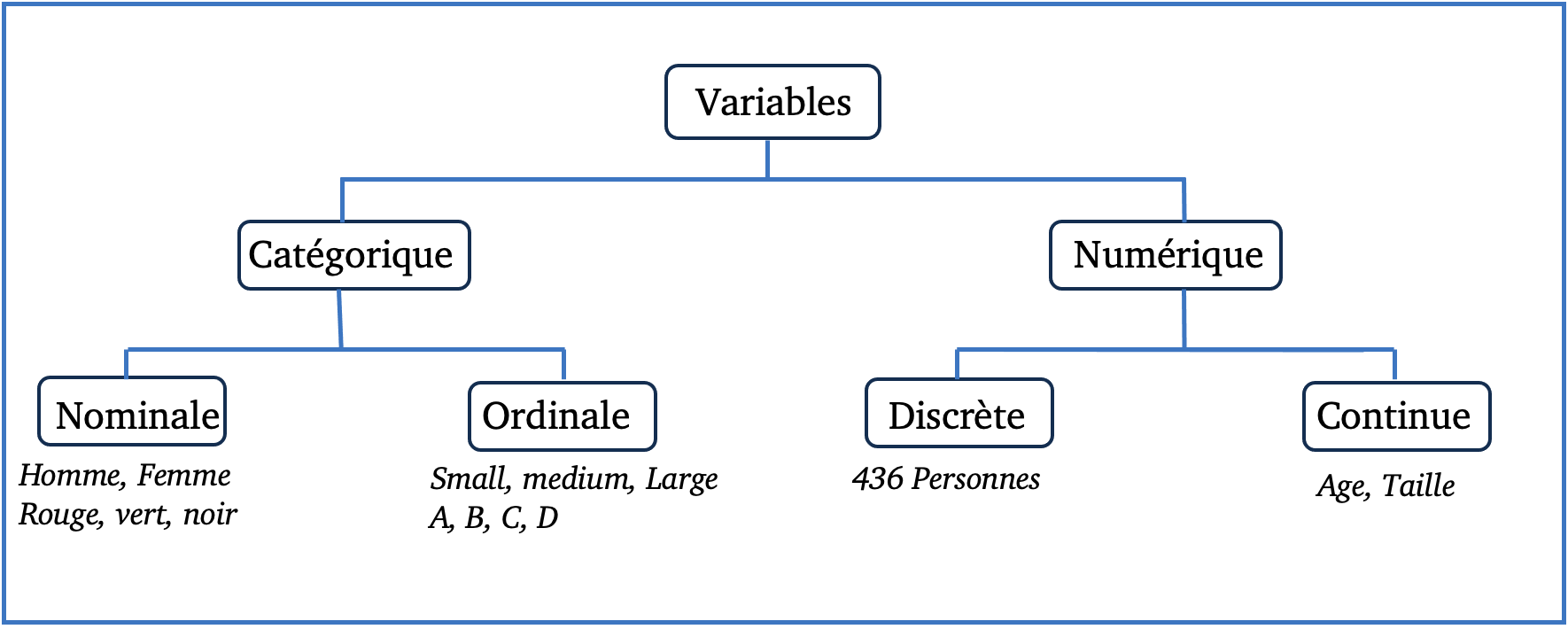
Vocabulaire autour de la variable :

Lors d’une analyse statistique, on distingue deux types principaux de variables :

La variable à expliquer (à prédir, ou à estimer) : Y
Les variables explicatives (prédictives ou estimatrices) : X_i

Tout l’exercice reside à établir la relation la plus pertinente entre les variables explicatives X_i et la variable à expliquer Y.

Tableau des synonymes :

Catégorique = Qualitative.
Numérique = Quantitative.

Exemple concret :

Je cherche à estimer le prix d’une maison en fonction de 4 caractéristiques : le type de bien, l’état du bien, le nombre de pièces et la superficie en m2.

Pour ce faire, j’ai à ma disposition une base de données intitulée “data_immobilier” (générée aléatoirement) que je traite en R.

Avant tout, je dois avoir ces éléments en tête :

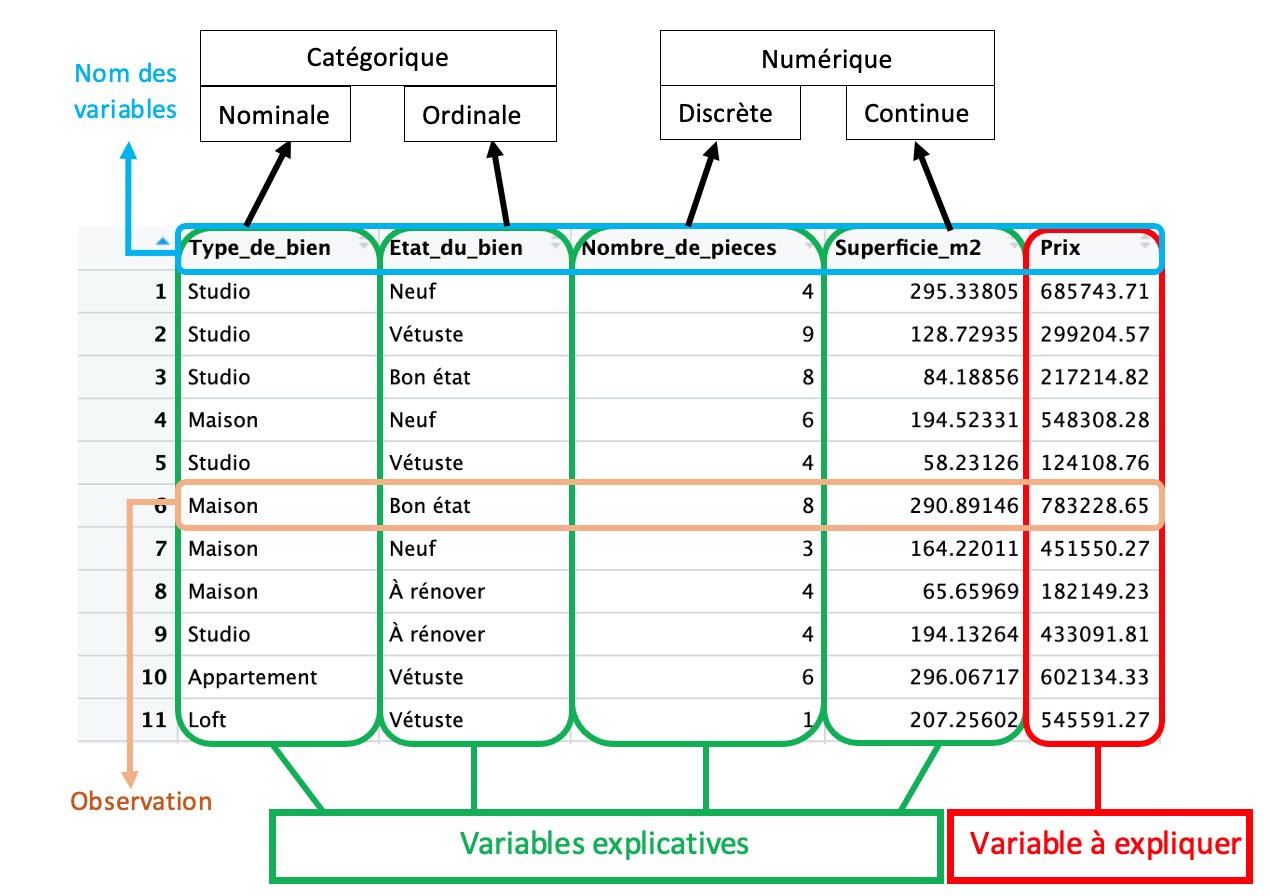
Ensuite, je peux passer à l’étape suivante.

Traitement des données

Peu importe leur origine, les bases de données nécessitent presque toujours un traitement avant d’être exploitables. De la collecte à l’enregistrement, des irrégularités s’introduisent, causant des erreurs lors de l’exploitation. Le traitement vise à corriger ou à gérer ces irrégularités. Bien que chaque base de données présente ses propres spécificités et problèmes, les quatre points que nous aborderons par la suite sont courants et doivent être maîtrisés

Gestion des valeurs manquantes

Les valeurs manquantes, souvent représentées par les NaN, sont parmi les anomalies les plus couramment rencontrées dans les bases de données. Plusieurs stratégies peuvent être adoptées face à ces valeurs :

Conversion : On surpasse le NaN en le convertissant en une autre valeur, comme un flottant.

Avantage : Conservation de données.
Désavantage : Introduction d’un biais potentiellement significatif.

Code :

# Convertir les NaN en 0 (ou une autre valeur) en R.
df[is.na(df)] <- 0

# Convertir les NaN en 0 (ou une autre valeur) en python. 
df.fillna(0, inplace=True)

imputation : remplacer les valeurs manquantes par des estimations (la moyenne ou la médiane des autres valeurs).

Avantage : Conservation de données.
Désavantage : Introduction d’un biais potentiellement significatif.

Code :

## Utiliser la moyenne pour imputer en R 
df$column_name[is.na(df$column_name)] <- mean(df$column_name, na.rm = TRUE)

# Utiliser la moyenne pour imputer en python
df['column_name'].fillna(df['column_name'].mean(), inplace=True)

suppression : supprimer les lignes avec des NaN.

Avantage : On limite le biais .
Désavantage : perte d’information générale.

Code :

# Supprimer les lignes contenant des NaN en R
df <- df[complete.cases(df), ]

# Supprimer les lignes contenant des NaN 
df.dropna(inplace=True)

Il n’y a pas de solution parfaite, certains cas vont favoriser certains choix, mais la suppression reste quand même la plus sur en terme de qualité de l’information, à privilègier des que possible.

Group_by

La fonction group_by est utilisé pour regrouper des données en fonction de certaines variables catégorielles. Cela permet d’effectuer des opérations et des analyses spécifiques à chaque groupe, et comprendre les comportements ou les anomalies spécifiques à chaque groupe.
Concretement, si l’on reprend la base data_immobilier, faire une group_by sur la variable Type_de_bien nous permettra de faire une etude sur le groupe maison, loft, appartement et studio séparemment.

R :

# Groupement des données par Type_de_bien et calcul de la moyenne des autres variables
data_grouped <- data_immobilier %>%                                 #Nouveau DataFrame "data_grouped"
  group_by(Type_de_bien) %>%                                        #Selection par groupe "Type de bien"
  summarise(                                                        #Affiche les infomations
    Prix_moyen = mean(Prix, na.rm = TRUE),                          #La moyenne de prix pour chaque groupe
    Superficie_moyenne = mean(Superficie_m2, na.rm = TRUE),         #La moyenne de superficie pour chaque groupe
    Nombre_moyen_de_pieces = mean(Nombre_de_pieces, na.rm = TRUE)   #La moyenne de Nombre de piece pour chaque groupe
  )
print(data_grouped)                                                 #Affichage

Python :

# Groupement des données par Type_de_bien et calcul de la moyenne des autres variables 
data_grouped = data_immobilier.groupby('Type_de_bien').agg({
    'Prix': 'mean',
    'Superficie_m2': 'mean',
    'Nombre_de_pieces': 'mean'
}).reset_index()
print(data_grouped)

Merge

La fonction merge est utilisée pour fusionner deux dataframes sur la base d’au moins une colonne commune. Cette fonction est extremement utile si l’on souhaite combiner des données provennant de differentes bases pour une même analyse.

Application concrète avec la base de données data_immobilier:
On a une autre base de données, data_Localisation, avec les variables Superficie_m2 et Localisation. En utilisant la fonction merge, on va fusionner les deux bases de données en utilisant la colonne commune, Superficie_m2 , pour avoir une base de données plus riche.

# Exemple de code R utilisant merge
data_complete <- merge(data_immobilier, data_Localisation, by = "Superficie_m2", all = TRUE)

# Exemple de code Python utilisant merge
data_complete = pd.merge(data_immobilier, data_Localisation, on='Superficie_m2', how='outer')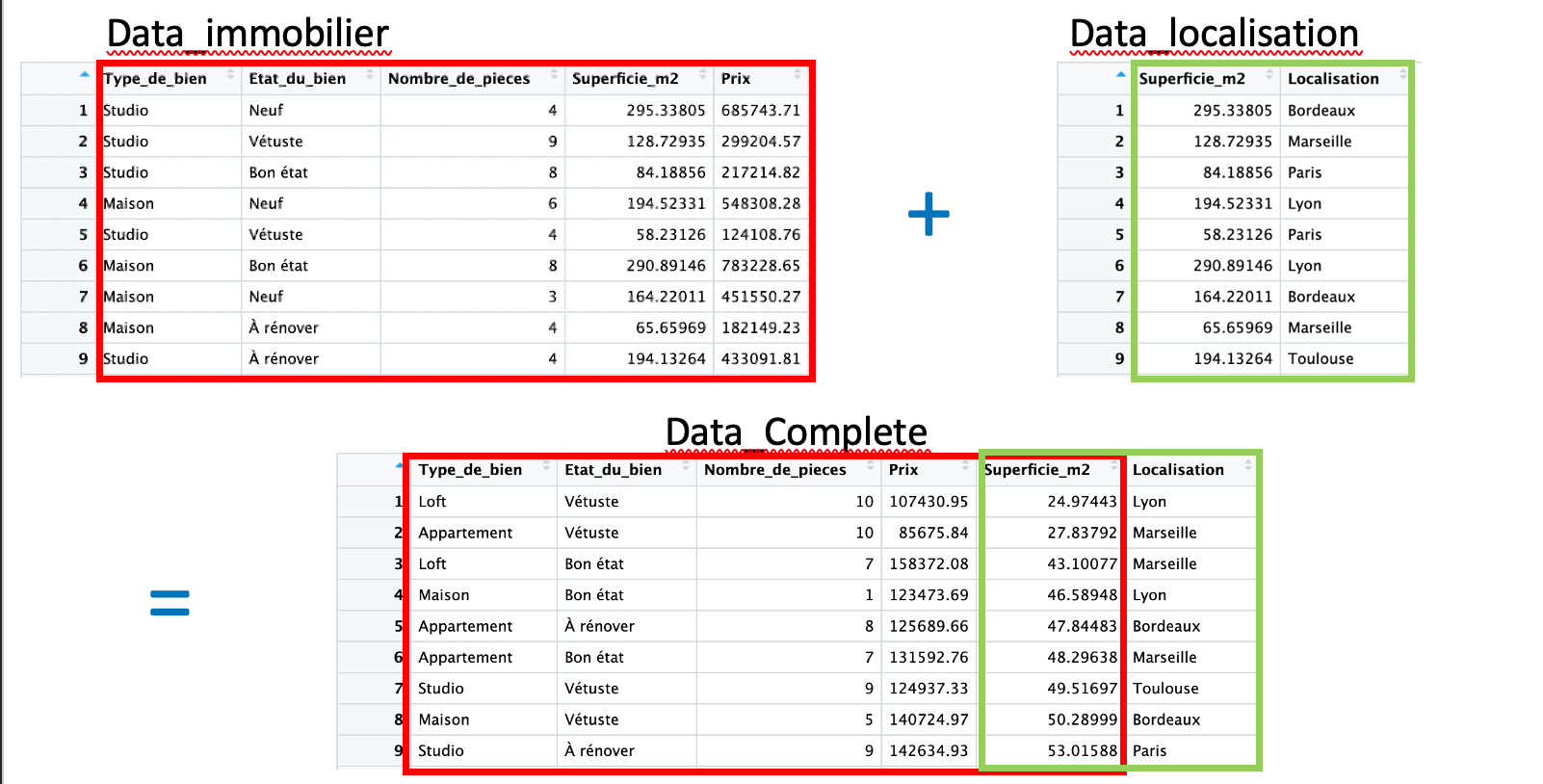

variables dummys

Les variables dummy sont utilisées pour convertir des variables catégorielles en variables numériques.
Objectifs : Utiliser ces variables dans des analyses statistiques et des modèles de machine learning qui requièrent des entrées numériques. Comment créer des variables dummy ? Exemple concret :

On reprend le dataframe qui a une desormais colonne catégorielle nommée Localisation avec des noms de villes. On crée les variables dummy, soit pour chaque catégorie unique dans la colonne Localisation deviendra une nouvelle colonne dans le dataframe.

# En R
data_with_dummies <- model.matrix(~ Localisation - 1, data = data_complete) %>% 
                     as.data.frame()

# En python
data_with_dummies = pd.get_dummies(data_complete, columns=['Localisation'], prefix='', prefix_sep='')

Dans le nouveau dataframe, data_with_dummies, chaque ville unique de la colonne Localisation originale a été transformée en une nouvelle colonne. Si une observation dans la colonne Localisation originale était “Paris”, alors la colonne LocalisationParis serait marquée avec un 1, et toutes les autres colonnes de ville seraient marquées avec des 0.

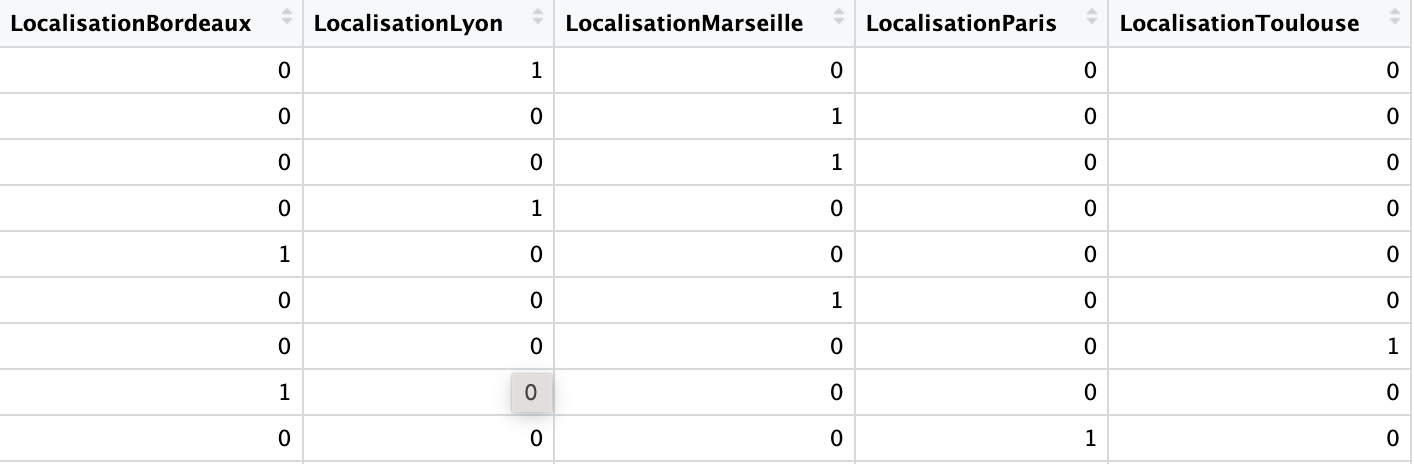
Attention aux problémes de multicolinéarité, supprimer une colonne pour une utilisation dans certains modèles.

Statistiques Descriptives

Les statistiques descriptives permettent de résumer, décrire et comprendre les données.

Pour les variables quantitatives, on utilise :

Moyenne : La valeur moyenne.
Médiane : La valeur centrale.
Mode : La valeur la plus fréquente.
Min,Max= valeur minimal et maximum. Écart Type : Mesure de la dispersion des valeurs.

# En python
describe(data_quantitative)

# En R 
summary(data_quantitative)

Pour les variables qualitatives, on utilise:

Fréquences : Nombre de fois qu’une catégorie apparaît.
Pourcentages : Proportion d’une catégorie par rapport au total.

# En python
# Calculer les fréquences
freq = data_qualitative.value_counts()
# Calculer les pourcentages
perce = frequencies / len(data_qualitative) * 100

# En R 
# Calculer les fréquences
frequencies <- table(data_qualitative)
# Calculer les pourcentages
percentages <- prop.table(frequencies) * 100

On illustre également par des graphiques descriptifs:

Histogrammes et Diagrammes en Barres : Pour montrer la distribution des données.
Boîtes à Moustaches (Boxplots) : Pour montrer la médiane, quartiles et valeurs aberrantes.

# En python
# Créer un histogramme pour les données quantitatives
plt.hist(data_quantitative, bins=5, edgecolor='k')
plt.xlabel("Valeurs")
plt.ylabel("Fréquence")
plt.title("Histogramme des données quantitatives")
plt.show()

# En R 
# Créer un histogramme pour les données quantitatives
ggplot(data = data.frame(x = data_quantitative)) +
  geom_histogram(aes(x = x), binwidth = 5, fill = "blue", color = "black") +
  labs(x = "Valeurs", y = "Fréquence", title = "Histogramme des données quantitatives")

La statistique descriptive offre une première compréhension des données, indispensable avant toute analyse plus approfondie. Elle permet de déceler des tendances, anomalies, ou relations à explorer davantage. C’est une étape indispensable à ne surtout pas negliger.

Premiers modèles

Modèles linéaires

Def regression : Un ensemble de méthodes pour analyser la relation d’une variable à expliquer par une ou plusieurs autres variables explicatives.

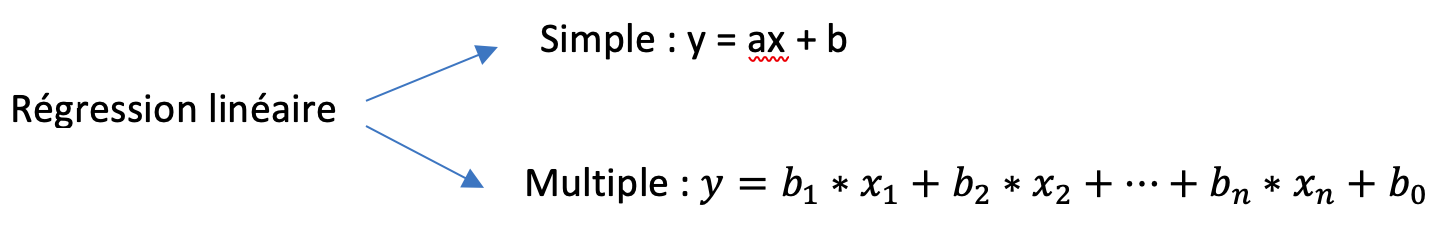
Méthode des moindres carrés ordinaires :

Objectif : Regarder à quel point la droite obtenue est meilleure que la droite de la moyenne des observations. Donc, \(R^2 = \min\left(\sum(y - \hat{y})^2\right)\)

Moindres carrés ajustés :

Le \(R^2\) carré ordinaire peut seulement augmenter ou rester constant par l’ajout d’une nouvelle variable. Concretement, ne réduira jamais la capacité explicative du modèle. Le adjusted - \(R^2\) est une methode par pénalisation qui compense ce défaut. Il faut donc le privilègier à l’etude.

P-value :

C’est un indicateur statistique utilisé pour évaluer la significativité d’un résultat. On pose que l’hypothèse nulle (généralement l’absence d’effet ou de relation) est vraie. Une p-value faible suggère que les observations sont peu probables sous l’hypothèse nulle, indiquant ainsi une évidence forte contre l’hypothèse nulle et en faveur de l’hypothèse alternative, donc qu’il y a probablement une relation.

Une p-value inférieure à un seuil défini (souvent 0,05) est généralement interprétée comme statistiquement significative, suggérant que le modèle ou la variable examinée a un effet réel et non dû au hasard.

Concrètement,

p-value < 5%, la variable est statistiquement significative, donc probablement explicative, on la garde dans le modèle.
p-value > 5%, la variable n’est pas statistiquement significative, donc probablement pas explicative, on l’exclut du modèle.

Gestion des outliers :

Certaines observations extrêmes, ou outliers, peuvent fausser les résultats en raison de leur décalage significatif par rapport au reste des données. Il faut les identifier et, si nécessaire, les exclure en amont de l’analyse. Pour ce faire, on utilise souvent des méthodes telles que DFFITS et DFBETAS. Ces techniques aident à déterminer si une observation individuelle est particulièrement influente et si elle devrait être considérée comme un outlier devant être exclu de l’analyse pour obtenir des résultats plus fiables.

Multicollinéarité :

La multicollinéarité dans les modèles de régression linéaire est un phénomène où deux ou plusieurs variables explicatives sont fortement corrélées entre elles. Cette forte corrélation peut causer des problèmes dans l’estimation des coefficients de régression, rendant les résultats moins fiables. Pour mesurer le degré de multicollinéarité dans un modèle, on utilise souvent l’indice VIF.

VIF < 5, peu de risque de multicollinéarité .
VIF > 5, risque de multicollinéarité.

Méthode Backward élimination pour affiner la précision du modèle :

Initialement, on a une variable à expliquer et plusieurs variables explicatives.

On cherche la meilleure combinaison possible entre ces variables pour definir ce modèle, du point de vue de la significativité à travers la p-value, et de l’explicativité à travers le adjusted- \(R^2\).

Une idée serait de tester toutes les combinaisons une à une, en théorie cela fonctionnerait, mais cela n’est pas réaliste au vu de la quantité de calcul nécessaire.

la méthode Backward élimination consiste alors à évaluer le modèle par itération suivant le schéma suivant :

1 - Je fais mon modèle avec l’ensemble des variables.
2 - Je supprime LA variable qui à la p-value > 5%, la plus élevé.
3 - Je réévalue le modèle
4 - Je regarde comment le adjusted-\(R^2\) à évoluer :
- Il augmente, c’est bien le modèle est plus explicatif
- Il diminue, c’est mauvais, la variable avait quand même une importance
  - Je refléchis à la conserver ou non si la p-value est pas trop haute.
5 - Je répète les étapes 2,3 et 4 autant de fois que nécessaire.

Codes :

Régression linéaire simple :

#var1 -> a expliquer
#var2 -> explicative

Reg1<-lm(var1~var2, data=df)
summary(Reg1) # Le détail 
abline(Reg1) #Representation de la regression linéaire

Régression linéaire multiple :

#var1 -> a expliquer

Reg1<-lm(var1~var2+var3+var4, data=df)
summary(Reg1) # Le détail 
abline(Reg1)  #Representation de la regression linéaire

Regression logistique

Def regression logistique : Utilisée pour des problèmes de classification ( variable dependante bianire ).

Principe: Modélise la probabilité que la variable dépendante appartienne à une catégorie particulière.

# Régression logistique en R (y binaire à expliquer)
glm_model <- glm(y ~ x1 + x2, data = dataset, family = "binomial")
summary(glm_model)

# Régression logistique en Python (y binaire à expliquer)
from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
model.fit(X, y)

Regression ridge et lasso

Rigde

Usage: Utilisée pour traiter le problème de multicollinéarité dans les données. Ajoute une pénalité au carré des coefficients. Principe: Minimise une somme pondérée des carrés des résidus et des carrés des coefficients.

# Régression Ridge en R
library(glmnet)
ridge_model <- glmnet(x, y, alpha = 0, lambda = lambda_value)

# Régression Ridge en Python
from sklearn.linear_model import Ridge

model = Ridge(alpha=1.0)
model.fit(X, y)

Lasso

Usage: Usage: Permet de sélectionner des variables en réduisant les coefficients de certaines à zéro. Principe: Semblable à Ridge, mais ajoute une pénalité absolue aux coefficients.

# Régression Lasso en R
library(glmnet)
lasso_model <- glmnet(x, y, alpha = 1, lambda = lambda_value)

# Régression Lasso en Python
from sklearn.linear_model import Lasso

model = Lasso(alpha=1.0)
model.fit(X, y)

Test d’independance

Les tests d’indépendance, sont utilisés en statistique pour déterminer si deux variables semblent être liées ou non. L’intérêt principal de ces tests est de vérifier l’existence d’une association ou d’une relation entre les variables.

Cas 1: Les deux variables sont nominales

# Tableaux des effectifs croisés ou fréquences croisées
tab <- table(var1, var2)
print(tab)
prop_table <- prop.table(tab, margin = 2)
print(prop_tab)

# Représentation graphique des profils
barplot(tab, legend = TRUE, beside = TRUE)
barplot(prop_table, legend = TRUE, beside = TRUE)

# Test d'indépendance du khi-carré
chi_sq_test <- chisq.test(tab)
print(chi_sq_test)

# Si chi_sq_test$p.value < 0.05 & all(chi_sq_test$expected > 5)
# Alors test significatif et effectifs espérés supérieurs à 5, il y a dependance. 

# Analyse des résidus standardisés via leur représentation avec la fonction mosaicplot()
mosaicplot(tab)

Cas 2: Une variable est quantitative et l’autre est nominale binaire

# var1 -> quantitative 
# var2 -> nominale binaire

# Sous-populations définies par la variable binaire
groupe1 <- df$var1[df$var2 == "Oui"]
groupe2 <- df$var1[df$var2 == "Non"]

# Indicateurs statistiques 
summary(groupe1)
summary(groupe2)

# Representation graphique
ggplot(df, aes(x = variable_nominale, y = variable_quantitative)) +
  geom_boxplot() +
  theme_minimal()

# Tester la normalité
shapiro1 <- shapiro.test(groupe1)
shapiro2 <- shapiro.test(groupe2)
print(shapiro1)
print(shapiro2)

# Si shapiro1$p.value > 0.05 et shapiro2$p.value > 0.05
# Normalité non rejetté 

# Procédure paramétrique

# Tester l'égalité des variances
var_test <- var.test(groupe1, groupe2)
print(var_test)

# Si var_test$p.value > 0.05
# Égalité des variances non rejeté 
# Faire un test de comparasion des moyennes 
t_test <- t.test(var_quanti ~ var_nominale, var.equal = TRUE)
print(t_test)

# Si var_test$p.value < 0.05
# Égalité des variances rejetée
# les variables ne sont pas indépendantes
# Faire un test de comparasion des moyennes 
t_test <- t.test(var_quanti ~ var_nominale, var.equal = FALSE)
print(t_test)

# Procédure non paramétrique (shapiro1$p.value < 0.05 ou shapiro2$p.value < 0.05)

# Tester l'égalité des variances
ansari_test <- ansari.test(groupe1, groupe2)
print(ansari_test)

# Si ansari_test$p.value > 0.05
# Égalité des variances non rejetée
# Faire un test de comparaison des medianes 
wilcox_test <- wilcox.test(var_quanti ~ var_nominale)
print(wilcox_test)

# Si ansari_test$p.value < 0.05
# Égalité des variances rejetée

"Les distributions conditionnelles de X connaissant Y diffèrent d'un paramètre d'échelle"

Cas 3 : une variable est quantitative et l’autre nominale non binaire

# var1 -> quantitative 
# var2 -> nominale non binaire

# Indicateurs statistiques
indicateurs <- df %>%
  group_by(var2) %>%
  summarise(moyenne = mean(var1),
            mediane = median(var1),
            ecart_type = sd(var1),
            minimum = min(var1),
            maximum = max(var1),
            q1 = quantile(var1, 0.25),
            q3 = quantile(var1, 0.75))
indicateurs

# Représentations graphiques
ggplot(df, aes(x = choux$var2, y = choux$var1)) +
  geom_boxplot(outlier.colour = "red", outlier.size = 2) +
  scale_fill_manual(values = c("lightgray", "lightblue"), guide = FALSE) +
  theme(axis.text.x = element_text(angle = 45, hjust = 1)) +
  labs(x = "", y = "Ventes ", title = "Boîtes à Moustaches des ...")

# Test de normalité
normality <- df %>%
  group_by(var2) %>%
  summarise(shapiro.test(var1)$p.value)
normality

# si tous les shapiro.test(var1)$p.value > 0.05
# Normalité non rejetté 
# procédure Paramétrique

bartlett_res <- bartlett.test(var1 ~ var2, data = df)
print(bartlett_res)

#si bartlett_res$p.value > 0.05 
#l’égalité des variances n’est pas rejetée

oneway_res <- oneway.test(var1 ~ var2, data = df, var.equal = TRUE)
print(oneway_res)

# Vérifier l'indépendance: 

##si oneway_res$p.value > 0.05
##alors Les variables sont indépendantes (pas de relation significative)

##si oneway_res$p.value < 0.05
##Les variables ne sont pas indépendantes (relation significative)

#si bartlett_res$p.value < 0.05 (l’égalité des variances est rejetée)
#Les variables ne sont pas indépendantes

#si au moins un shapiro.test(tonnage)$p.value < 0.05
#Procédure Non paramétrique

fligner_res <- fligner.test(var1 ~ var2, data = df)
print(fligner_res)

#si fligner_res$p.value > 0.05 

##l’égalité des variances n’est pas rejetée
kruskal_res <- kruskal.test(var1 ~ var2, data = df)
print(kruskal_res)

## Vérifier l'indépendance

## Si kruskal_res$p.value > 0.05
##Les variables sont indépendantes (pas de relation significative)

## Si kruskal_res$p.value < 0.05
##Les variables ne sont pas indépendantes (relation significative)

## Comparaison deux-à-deux
pairwise_wilcox_res <- pairwise.wilcox.test(df$var_quanti, df$var_nominale)
print(pairwise_wilcox_res)

#si fligner_res$p.value > 0.05 
#l’égalité des variances est rejetée

'Les distributions conditionnelles de X connaissant Y diffèrent d un paramètre d echelle'

Cas 4 :Les deux variables sont quantitatives

# Indicateurs statistiques
summary(var1)
summary(var2)

# Représentation du nuage de points
ggplot() +
  geom_point(aes(x = var1, y = var2)) +
  theme_minimal()

# Tester la normalité des couples d'observations
mshapiro_test <- shapiro.test(cbind(var1, var2))
print(mshapiro_test)

# Si mshapiro_test$p.value > 0.05
# Normalité non rejeté

## Test de non-corrélation de Pearson
pearson_test <- cor.test(var1, var2, method = "pearson")
print(pearson_test)

## Si la p-value < 0,05 on peut rejeter l'hypothèse nulle de non-corrélation, 
## Conclure qu'il y a une corrélation significative entre les deux variables

# Si mshapiro_test$p.value < 0.05
# Normalité rejetée

# Test de non-corrélation monotone de Spearman
spearman_test <- cor.test(var1, var2, method = "spearman")
print(spearman_test)

# Si la p-value < 0,05 on peut rejeter l'hypothèse nulle de non-corrélation, 
# Conclure qu'il y a une corrélation significative entre les deux variables