DATA Camp M1

Algèbre Linéaire : niveau élémentaire

Matrices

Une matrice est un tableau de nombres disposés en \(m\) lignes et \(n\) colonnes. Soit \(A\) de taille \((m, n)\) : \[ A = (a_{ij})_{i=1,\ldots,m \atop j=1,\ldots,n} = \begin{bmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & \cdots & a_{mn} \end{bmatrix} \]

Le terme \(a_{ij}\) est situé à la \(i\)-ème ligne de la \(j\)-ème colonne de la matrice \(A\).

\[ A = \begin{bmatrix} -2 & 1 \\ 8 & -3 \\ 1 & 3 \end{bmatrix} ;\quad B = \begin{bmatrix} -2 \\ -3 \\ 5 \end{bmatrix} ;\quad C = \begin{bmatrix} 3 & -1 & 6 \end{bmatrix} ;\quad D = \begin{bmatrix} 3 & -1 \\ 4 & -3 \end{bmatrix} \]

\(A\) est une matrice de taille \((3, 2)\), \(B\) est une matrice de taille \((3, 1)\), \(C\) est une matrice de taille \((1, 3)\), \(D\) est une matrice de taille \((2, 2)\).

Une matrice \((m, 1)\) est dite matrice colonne. Une matrice \((1, n)\) est dite une matrice ligne. Une matrice \((n, n)\) est dite une matrice carrée d’ordre \(n\).

On appelle transposée de \(A\) (et on note \(A^t\) ou \(A'\)), la matrice dont les lignes sont les colonnes de \(A\), et dont les colonnes sont les lignes de \(A\).

\[ A = \begin{bmatrix} -2 & 1 \\ 8 & -3 \\ 1 & 3 \end{bmatrix} \Rightarrow A^t = \begin{bmatrix} -2 & 8 & 1 \\ 1 & -3 & 3 \end{bmatrix} \]

\[ (A + B)^t = A^t + B^t \] \[ (AB)^t = B^t A \]

Matrices usuelles

Une matrice carrée d’ordre \(n\) est dite diagonale lorsque, pour tout \(i \neq j\), on a \(a_{ij} = 0\) : \[ A = \begin{bmatrix} -2 & 0 & 0 \\ 0 & -3 & 0 \\ 0 & 0 & 5 \end{bmatrix} \]

La matrice unité \(I_n\) est la matrice diagonale telle que \(\forall i = 1, \ldots, n\), \(a_{ii} = 1\) : \[ I_3 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \]

Opérations de base

Soient \(A\) et \(B\) deux matrices de même taille \((m, n)\) de termes généraux respectifs \(a_{ij}\) et \(b_{ij}\), et \(\lambda\) un nombre réel.

\(A = B\) si et seulement si \(a_{ij} = b_{ij}\) pour tous \(i,j\).

La somme de \(A\) et \(B\) est la matrice de terme général \(a_{ij} + b_{ij}\)

\[ A + B = \begin{bmatrix} 5 + (-4) & 2 + 1 \\ 6 + 1 & 1 + (-3) \end{bmatrix} = \begin{bmatrix} 1 & 3 \\ 7 & -2 \end{bmatrix} \]

Le produit de \(A\) par \(\lambda\) est la matrice de terme général \(\lambda a_{ij}\) : \[ \lambda A = 3 \times \begin{bmatrix} 5 & 2 \\ 6 & 1 \end{bmatrix} = \begin{bmatrix} 15 & 6 \\ 18 & 3 \end{bmatrix} \]

\[ A = \begin{bmatrix} 5 & 2 \\ 6 & 1 \end{bmatrix} ;\quad B = \begin{bmatrix} -4 & 1 \\ 1 & -3 \end{bmatrix} ;\quad \lambda = 3 \] \[ A + B = \begin{bmatrix} 1 & 3 \\ 7 & -2 \\ \end{bmatrix} \hspace{2cm} \lambda A = \begin{bmatrix} 15 & 6 \\ 18 & -2 \\ \end{bmatrix} \]

Multiplication matricielle

Le produit de matrices A et B (noté \(AB\)) n’est défini que si le nombre de colonnes de \(A\) est égal au nombre de lignes de \(B\). C’est-à-dire \(A\) doit être de taille \((m, p)\) et \(B\) de taille \((p, n)\). Alors \(AB\) est de taille \((m, n)\). De plus, soient \(a_{ij}\) et \(b_{ij}\) les termes généraux respectifs de \(A\) et \(B\), alors le terme général de \(C\) = \(AB\) est \(c_{ij}\) défini par : \[ c_{ij} = \sum_{k=1}^{p} a_{ik} b_{kj} \] \[A = \begin{bmatrix} 2 & -2 & 1 \\ -3 & 6 & 8 \\ 5 & 2 & 1 \end{bmatrix} \hspace{2cm} B = \begin{bmatrix} -1 & 5 \\ 1 & 2 \\ 3 & 4 \end{bmatrix}\] Alors, la matrice \(C = AB\) est donnée par : \[C = \begin{bmatrix} -1 & 10 \\ 33 & 29 \\ 0 & 33 \end{bmatrix}\]

En effet, l’élément qui se trouve au croisement de la i-ème ligne et la j-ème colonne est : \[c_{ij} = \sum_{k=1}^{p} a_{ik} b_{kj}\]

Par exemple, \[c_{2,1} = (-3) \times (-1) + 6 \times 1 + 8 \times 3 = 33\]

Propriétés

Le produit est distributif par rapport à l’addition. C’est-à-dire : \[ A (B + C) = AB + AC \quad \text{et} \quad (B + C)A = BA + CA \]

Le produit est associatif, c’est-à-dire : \[ ABC = A(BC) = (AB)C \]

Si A est une matrice carrée d’ordre n, alors \[A I_n = I_n A = A\]

Le produit de deux matrices peut être nul sans que l’une des deux matrices ne soit la matrice nulle, par exemple : \[ \begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix} \times \begin{bmatrix} -2 & 10 \\ 1 & -5 \end{bmatrix} \]

Inverse

Une matrice carrée \(A\) d’ordre \(n\) est dite inversible lorsqu’il existe une matrice \(B\) telle que : \[ A B = B A = I_n \] \(B\) est alors notée \(A^{-1}\), l’inverse de \(A\).

Systèmes linéaires

Grâce au produit matriciel, on peut représenter un système linéaire par une équation matricielle. Soit le système linéaire de \(n\) équations et \(p\) inconnues :

\[ \begin{cases} a_{11} x_1 + a_{12} x_2 + \ldots + a_{1p} x_p = b_1 \\ a_{21} x_1 + a_{22} x_2 + \ldots + a_{2p} x_p = b_2 \\ a_{n1} x_1 + a_{n2} x_2 + \ldots + a_{np} x_p = b_n \end{cases} \]

On peut le représenter par \(AX = B\) où :

\[A = \begin{bmatrix} a_{11} & \ldots & a_{1p} \\ \vdots & \ddots & \vdots \\ a_{n1} & \ldots & a_{np} \end{bmatrix} ; \hspace{2cm} X = \begin{bmatrix} x_1 \\ \vdots \\ x_p \end{bmatrix} ; \hspace{2cm} B = \begin{bmatrix} b_1 \\ \vdots \\ b_n \end{bmatrix}\]

Algèbre linéaire : niveau basique

Déterminant

Soit \(A = (a_{ij})\) une matrice carrée d’ordre 2. Le déterminant de \(A\) est le réel noté \(\text{det}(A)\) tel que : \[ \text{det}(A) = \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix} = a_{11}a_{22} - a_{12}a_{21} \]

Soient \(A = (a_{ij})\) et \(B = (b_{ij})\) deux matrices carrées d’ordre \(n\) et \(\lambda \in \mathbb{R}\). On a les propriétés suivantes :

• \(\text{det}(AB) = \text{det}(A) \cdot \text{det}(B) = \text{det}(BA)\)
• \(\text{det}(A^T) = \text{det}(A)\)
• \(\text{det}(\lambda A) = \lambda^n \cdot \text{det}(A)\)
• Si \(A\) est diagonale, alors \(\text{det}(A) = a_{11}a_{22}\ldots a_{nn}\)
• \(\text{det}(I_n) = 1\)
• \(A\) est inversible si et seulement si \(\text{det}(A) \neq 0\)
• Si \(\text{det}(A) \neq 0\), alors \(\text{det}(A^{-1}) = \frac{1}{\text{det}(A)}\)

Diagonalisation

Une valeur propre de \(A\) est un scalaire \(\lambda\) tel qu’il existe un vecteur colonne non nul \(V\) vérifiant : \(AV = \lambda V\). \(V\) est alors appelé vecteur propre de \(A\) associé à \(\lambda\).

Une matrice carrée \(A\) d’ordre \(n\) est diagonalisable lorsqu’il existe une matrice diagonale \(D\) et une matrice inversible \(P\) telles que : \(A = PDP^{-1}\). \(D\) est constituée des valeurs propres de \(A\). \(P\) est obtenue par la concaténation des vecteurs propres de \(A\). Si les valeurs propres de \(A\) sont distinctes, alors \(A\) est diagonalisable (réciproque fausse).

Matrice symétrique

Une matrice carrée \(A\) d’ordre \(n\) est symétrique lorsque \(A^T = A\). Si \(A\) est symétrique, alors :

• \(A\) a des valeurs propres réelles.
• \(A\) est diagonalisable.
• Il existe une matrice \(P\) telle que \(P^{-1} = P^T\) et \(A = PDP^{-1}\).

Produit scalaire

Soit \(x\), \(y\), \(z\) trois vecteurs de \(\mathbb{R}^n\) et \(\lambda\) un scalaire. On définit par produit scalaire (qu’on note \(\langle \cdot, \cdot \rangle\)) toute application qui vérifie les propriétés suivantes :

• \(\langle x + \lambda y, z \rangle = \langle x, z \rangle + \lambda \langle y, z \rangle\)
• \(\langle x, y + \lambda z \rangle = \langle x, z \rangle + \lambda \langle x, z \rangle\)
• \(\langle x, y \rangle = \langle y, x \rangle\)
• \(\langle x, x \rangle \geq 0\)
• \(\langle x, x \rangle = 0 \Rightarrow x = 0\)

Le produit scalaire canonique et usuel est défini comme : \[ \langle x, y \rangle = \sum_{i=1}^{n} x_i \cdot y_i \]

Norme

On appelle norme associée à un produit scalaire le réel \(\|x\| = \sqrt{\langle x, x \rangle}\). Elle vérifie les propriétés suivantes :

• \(|\langle x, y \rangle| \leq \|x\| \cdot \|y\|\) (Inégalité de Cauchy-Schwartz)
• \(\|x + y\| \leq \|x\| + \|y\|\) (Inégalité triangulaire)
• \(\|x\| \geq 0\) avec égalité si \(x = 0\)
• \(\|\lambda x\| = |\lambda| \cdot \|x\|\)
• \(\|x + y\|^2 = \|x\|^2 + \|y\|^2 + 2\langle x, y \rangle\)

Un vecteur est dit unitaire ou normé si \(\|x\| = 1\)

Orthogonalité

Deux vecteurs \(x\) et \(y\) sont dits orthogonaux si \(\langle x, y \rangle = 0\). On note \(x \perp y\).

Une famille de vecteurs \(\{x_i\}\) est dite orthogonale si tous ses vecteurs sont deux à deux orthogonaux. Toute famille orthogonale \(\{x_i\}_{i=1}^p\) vérifie le théorème de Pythagore : \[ \left\|\sum_{i=1}^n x_i\right\|^2 = \sum_{i=1}^n \|x_i\|^2 \]

Soit \(E\) un espace muni d’un produit scalaire et \(X\) une partie de \(E\). On appelle orthogonal de \(X\) et on note \(X^\perp\) l’ensemble : \(X^\perp = \{y \in E \,|\, \forall x \in X, \langle x, y \rangle = 0\}\).

On dit que \(\{e_i\}_{i=1}^p\) est une base orthonormée de \(E\) si et seulement si : - Si \(a_1e_1 + a_2e_2 + \ldots + a_ne_n = 0\), alors \(a_i = 0\) pour tout \(i \in \{1, \ldots, n\}\).
- Pour tout \(x \in E\), il existe \(a_1, a_2, \ldots, a_n \in \mathbb{R}\) tels que \(x = a_1e_1 + a_2e_2 + \ldots + a_ne_n\).
- \(e_i\) est orthogonal à \(e_j\) pour tout \(i \neq j\).
- Pour tout \(i \in \{1, \ldots, n\}\), \(\|e_i\| = 1\).

Projection orthogonale

Soit \(x\) un vecteur d’un espace muni d’un produit scalaire \(E\). Soit \(F\) un sous-espace vectoriel de \(E\), \(x\) s’écrit de façon unique sous la forme : \(x = f + f^\perp\) où \(f \in F\) et \(f^\perp \in F^\perp\). On dit que \(f\) est le projeté orthogonal de \(x\) sur \(F\) et on note \(f = P_F(x)\).

Pour \(x\) et \(y\) de \(E\), on a \(\langle P_F(x),y\rangle = \langle x, P_F(y)\>\).

Si \((e_1, e_2, \ldots, e_n)\) est une base orthonormée, alors : \(P_F(x) = \sum_{i=1}^n \langle x, e_i \rangle e_i\)

Notons que : \(\|x - P_F(x)\| = \inf_{f \in F} \|x - f\|\)

Matrice orthogonale

Soit \(M\) une matrice carrée d’ordre \(n\). On dit que \(M\) est une matrice orthogonale si elle vérifie : \[M \cdot M^T = M^T \cdot M = I_n\]

Le déterminant d’une matrice orthogonale est égal à \(\pm 1\). L’ensemble des valeurs propres de \(M\) est inclus dans l’ensemble \(\{0, 1\}\).

Fondements de probabilité : niveau élémentaire

Quelques définitions

• On appelle épreuve \(E\) toute expérience probabiliste.
• On appelle univers de \(E\) l’ensemble, généralement noté \(\Omega\), de tous les résultats possibles de l’épreuve \(E\) (appelés “événements élémentaires”).

Lancer une paire de dés équilibrés et en retenir la somme est une épreuve. \(\Omega = \{2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\}\)

Evénements

Un événement est un sous-ensemble de \(\Omega\).

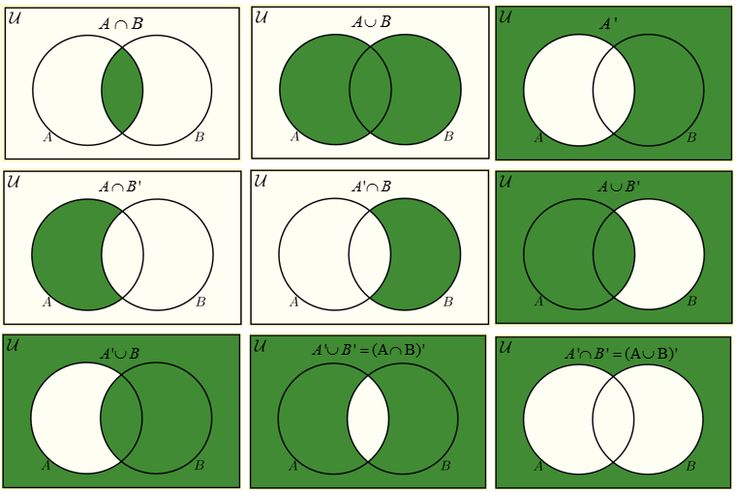
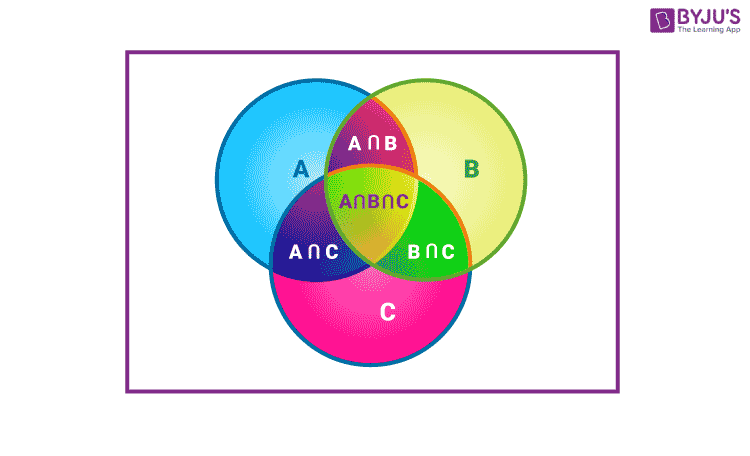
• L’intersection de \(A\) et \(B\), notée \(A \cap B\), est un événement. Il est réalisé uniquement si \(A\) et \(B\) se produisent.
• La réunion de \(A\) et \(B\), notée \(A \cup B\), est un événement. Il est réalisé si \(A\) ou \(B\) se produit. Deux événements remarquables sont à retenir :
  • L’événement certain \(\Omega\) ;
  • L’événement impossible \(\emptyset\) ;
• Tous les éléments qui n’appartiennent pas à \(A\) appartiennent à un événement que l’on appelle le complémentaire de \(A\). On le note \(\overline{A}\) ou \(A^C\).
• On dit que deux événements \(A\) et \(B\) sont incompatibles s’ils ne peuvent pas être réalisés en même temps.

Si \(A\), \(B\) et \(C\) sont des événements de \(\Omega\), les propriétés suivantes sont toujours vérifiées :

• \(A \cup \overline{A} = \Omega\) et \(A \cap \overline{A} = \emptyset\)
• \(\overline{\overline{A} \cap \overline{B}} = \overline{A} \cup \overline{B}\) et \(\overline{\overline{A} \cup \overline{B}} = \overline{A} \cap \overline{B}\) (lois de De Morgan)
• \(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\)
• \(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\)

Partitions

La famille d’événements forme une partition de \(\Omega\) si : \[ \bigcup_{i \in I} A_i = \Omega \quad \text{et} \quad A_i \cap A_j = \emptyset \text{ pour tout } i \neq j. \] Une partition remarquable est la famille qui contient l’événement \(A\) et son complémentaire.

Tribus et boréliens

Une tribu est une famille \(T\) de parties de l’ensemble \(\Omega\) qui vérifie les propriétés suivantes : - \(\Omega \in T\)
- Si \((A_n)\) est une suite dénombrable d’éléments de \(T\), alors \(\bigcup A_n \in T\)
— Si \(A\) est un élément de \(T\), alors son complémentaire l’est aussi.

De plus, si \(T\) est une tribu, alors : - \(\emptyset \in T\)
- Si \((A_n)\) est une suite d’éléments de \(T\), alors \(\bigcap A_n \in T\).

Pour le cas discret, on considère l’expérience “Lancer une pièce de monnaie équilibrée”.
On notera : \(P\) pour “PILE apparaît” et \(F\) pour “FACE apparaît”.
Dans ce cas, l’univers est l’ensemble \(\{P, F\}\) et \(T = \{\Omega, \emptyset, P, F\}\) est une tribu.
En général, l’ensemble des parties est une tribu classique.

Pour le cas continu, les intervalles du type \([a, +\infty[\), \(]a, +\infty[\), \(]-\infty, a[\), \(]-\infty, a]\) sont des tribus. Nous les appelons DES BORÉLIENS.

Soient \(A\) et \(B\) deux événements. Les propriétés suivantes sont toujours vraies :

1. \(P(A^C) = 1 - P(A)\)
   
2. \(P(B) = P(A \cap B) + P(A^C \cap B)\)
   
3. Si \(A \subset B\), alors \(P(A) \leq P(B)\)
   
4. \(0 \leq P(A) \leq 1\)
   
5. \(P(A \cup B) = P(A) + P(B) - P(A \cap B)\)

De plus, en considérant une suite \((A_k)\) d’événements, on a les relations suivantes : \[ \begin{aligned} P\left(\bigcup A_k\right) & = \lim_{n \to +\infty} P\left(\bigcup_{k=1}^n A_k\right) \\ P\left(\bigcap A_k\right) & = \lim_{n \to +\infty} P\left(\bigcap_{k=1}^n A_k\right) \\ P\left(\bigcup A_k\right) & \leq \sum_{k=1}^{+\infty} P(A_k) \end{aligned} \]

Et si \(\bigcup A_k = \Omega\), alors : \[ P(B) = \sum_{k=1}^{+\infty} P(B \cap A_k) \]

Mesure

Soit \(E\) un ensemble muni d’une tribu \(T\). On appelle mesure toute application \(m : T \rightarrow \mathbb{R}^+\) telle que : - \(m(\emptyset) = 0\) - Si \((A_n)\) est une suite d’éléments de \(T\) deux à deux disjoints alors : \[m\left(\bigcup_n A_n\right) = \sum_n m(A_n).\]

Probabilités

Soit \(E\) un ensemble muni d’une tribu \(T\). On appelle probabilité toute application \(P : T \rightarrow \mathbb{R}^+\) telle que : - \(P(\emptyset) = 0\) - Si \((A_n)\) est une suite d’éléments de \(T\) deux à deux disjoints alors : \[P\left(\bigcup_n A_n\right) = \sum_n P(A_n).\]

Probabilités conditionnelles

En théorie des probabilités, nous nous intéressons souvent au comportement d’un aléa, sachant qu’un autre événement est déjà passé. C’est ce que nous appelons Les Probabilités Conditionnelles.

Considérant deux événements de probabilité non nulle, \(A\) et \(B\), la probabilité conditionnelle de \(A\) sachant que \(B\) est réalisé (couramment dit \(A\) sachant \(B\)) est donnée par : \[ P(A|B) = \frac{P(A \cap B)}{P(B)} \]

Par commutativité de l’intersection, nous avons : \[ P(A \cap B) = P(B \cap A) \]

En utilisant la formule ci-dessus, nous pouvons également exprimer la probabilité conditionnelle de \(B\) sachant \(A\) : \[ P(B|A) = \frac{P(A|B) \cdot P(B)}{P(A)} \]

C’est ce que nous appelons .

Indépendance

Deux événements \(A\) et \(B\) sont dits indépendants si et seulement si : \[P(A \cap B) = P(A) \cdot P(B)\] En termes courants, deux événements sont indépendants si le résultat de l’un n’influence aucunement l’aboutissement de l’autre. Sous condition d’indépendance de \(A\) et \(B\), la notion de la probabilité conditionnelle tombe à l’eau, car les événements évoluent l’un sans se soucier de l’autre. Ceci se traduit par : \[P(A|B) = P(A)\] \[P(B|A) = P(B)\]

Notons que si \(A\) est indépendant de \(B\), il le sera par rapport à son complémentaire également, et vice versa. En général, pour une suite \((A_n)\) d’événements indépendants, on a : \[P\left(\bigcap A_i\right) = \prod P(A_i) = P(A_1) \cdot \ldots \cdot P(A_n)\] Cette formule est largement utilisée en statistique.

Variable aléatoire

Une variable aléatoire est un nombre qui dépend du résultat d’une expérience aléatoire. Chaque exécution de l’expérience génère une réalisation de la variable aléatoire.

Mathématiquement, on définit une variable aléatoire X comme une fonction \(X : T \rightarrow \mathbb{R}\) qui associe à chaque événement s, un réel \(X(s)\).

Par exemple, dans une queue pour la caisse d’un magasin, le nombre de clients est une variable aléatoire. La durée de traitement de chaque requête aussi. Remarquons que la première est un nombre entier. On dit qu’elle est à support discret. Alors que la deuxième est une durée (un nombre réel). On dit qu’elle est à support continu.

Fonction de répartition

Une variable aléatoire traduit le résultat d’une expérience aléatoire en nombre réel. La fonction de répartition transporte le calcul des probabilités concernant les réalisations de la variable aléatoire. C’est la fonction définie par : \[F_X(x) = P(X \leq x)\]

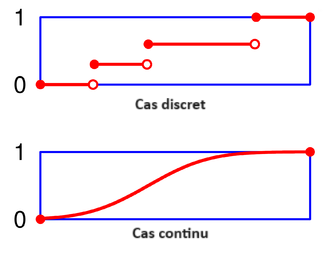
Pour tout \(x\), \(0 \leq F_X(x) \leq 1\) \(F_X\) est une fonction croissante. \(\lim_{x \to -\infty} F_X(x) = 0\) et \(\lim_{x \to \infty} F_X(x) = 1\)

Probabilité ponctuelle / Densité

La probabilité ponctuelle est la fonction qui décrit les sauts de la fonction de répartition : \[P(X = k) = P(X \leq k) - P(X \leq k - 1) = p_k\] \[\sum p_i = 1\]

La densité est la fonction qui décrit les variations de la fonction de répartition : \[f(x) = \frac{dF_X}{dx}(x)\] \[\int f(x) dx = 1\]

Fondements de probabilités : niveau basique

Moments

L’espérance d’une variable aléatoire est sa valeur attendue. C’est une mesure de localisation de la distribution.

Dans le cas discret : \[E(X) = \sum k \cdot P(X = k)\] \[k \in X(\Omega)\] Alors que dans le cas continu : \[E(X) = \int x \cdot f_X(x) \, dx\] \[x \in X(\Omega)\]

\[E(g(X)) = \sum g(k) \cdot P(X = k)\] \[\forall k \in X(\Omega)\] \[E(g(X)) = \int g(x) \cdot f_X(x) \, dx\] \[\forall x \in X(\Omega)\]

La variance d’une variable aléatoire décrit la dispersion de la variable aléatoire autour de sa valeur moyenne (son espérance).

Elle est définie par : \[Var(X) = E(X^2) - (E(X))^2 = E((x - E(X))^2)\] Sa racine carrée est appelée écart-type et notée généralement : \[\sigma(X) = \sqrt{Var(X)}\]

Le centrage consiste à localiser la distribution autour de l’origine et la réduction consiste à normaliser la dispersion. La technique est simple : \[Y = \frac{X - E(X)}{\sigma(X)}\]

Le moment d’ordre r est défini par : \[\mu_r = E(X^r)\] Le moment centré d’ordre r est défini ainsi : \[\mũ_r = E((X - E(X))^r)\]

Couples aléatoires

La fonction conjointe \[F_{X, Y}(x, y) = P(X \leq x \cap Y \leq y)\] est appelée la distribution conjointe de X et Y.

Dans le cas continu, la fonction définie par : \[f_{X, Y}(x, y) = \frac{\partial^2 F_{X, Y}(x, y)}{\partial x \partial y}\] est la densité conjointe du couple (X, Y). On a donc : \[F_{X, Y}(x, y) = \int \int f_{X, Y}(t, u) \, dt \, du, \text{ où } -\infty < x, y < +\infty,\]

Dans le cas discret, on définit la fonction de probabilité conjointe : \[P(X = x_i, Y = y_j) = p_{ij}\] On a donc : \[F_{X, Y}(x, y) = \sum \sum p_{ij}, \text{ où } x_i \leq x \text{ et } y_j \leq y\]

La loi marginale de X est définie comme suit : \[f_X(x) = \int f_{X, Y}(x, y) \, dy, \text{ où } -\infty < x < \infty,\] dans le cas continu, ou encore : \[f_X(x_i) = \sum p_{ij}, \text{ où } j \text{ tel que } y_j \leq y\]

Si X et Y sont indépendants, alors : \[f_{X, Y}(x, y) = f_X(x) \cdot f_Y(y)\]

La covariance mesure l’intensité de la relation linéaire entre deux variables aléatoires X et Y. Elle est définie comme suit : \[Cov(X, Y) = E(XY) - E(X) \cdot E(Y)\]

Si X et Y sont indépendants, alors : \[Cov(X, Y) = 0\]

Propriétés

\[ \mathbb{E}(aX + bY) = a\mathbb{E}(X) + b\mathbb{E}(Y) \] \[ \mathbb{E}(a) = a \]

\[ \text{Var}(aX) = a^2\text{Var}(X) \] \[ \text{Var}(a) = 0 \] \[ \text{Var}(X + Y) = \text{Var}(X) + \text{Var}(Y) + 2\text{Cov}(X,Y) \] \[ \text{Var}(X - Y) = \text{Var}(X) + \text{Var}(Y) - 2\text{Cov}(X,Y) \]

\[ \text{Cov}(X, Y) = \text{Cov}(Y, X) \] \[ \text{Cov}(aX + b, cY + d) = ac\text{Cov}(X, Y) \] \[ \text{Cov}(aX + bY, U) = a\text{Cov}(X, U) + b\text{Cov}(Y, U) \] \[ \text{Cov}(X, cU + dV) = c\text{Cov}(X, U) + d\text{Cov}(X, V) \] \[ \text{Cov}(aX + bY, cU + dV) = ac\text{Cov}(X, U) + ad\text{Cov}(X, V) + bc\text{Cov}(Y, U) + bd\text{Cov}(Y, V) \]

Vecteurs aléatoires

Pour un vecteur aléatoire \[(X_1, X_2, \ldots, X_n)\], l’espérance est toujours linéaire. Pour une suite \[(a_i)_{i \in \{1, \ldots, n\}}\] de réels, on a : \[ \mathbb{E}(a_1X_1 + a_2X_2 + \ldots + a_nX_n) = a_1\mathbb{E}(X_1) + a_2\mathbb{E}(X_2) + \ldots + a_n\mathbb{E}(X_n) \]

Si les variables aléatoires \[X_1, X_2, \ldots, X_n\] sont indépendantes, alors la variance de leur somme est égale à la somme de leurs variances individuelles : \[ \text{Var}(X_1 + X_2 + \ldots + X_n) = \text{Var}(X_1) + \ldots + \text{Var}(X_n) \]

Lois usuelles

Ces tableaux récapitulent les lois usuelles que vous pourrez rencontrer dans différents cours du master.

\[\Gamma(x) = \int_0^{\infty} t^{x-1}e^{-t} \, dt \text{ : désigne la fonction Gamma d'Euler}\]

\[B(x, y) = \frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)} \text{ : désigne la fonction Bêta}\]

Nous allons souvent rencontrer les lois grisées dans les Tests statistiques. Là encore, connaître les densités ne servirait pas à grand chose, mais ceci nous évitera de parler de lois dont nous ne connaissons pas la tête.

Fondements de probabilités

Vecteurs aléatoires

Les variables \(X_1, \ldots, X_n\) sont deux à deux indépendantes si et seulement si : \(\forall i \neq j, X_i\) et \(X_j\) sont indépendantes.

Les variables \(X_1, \ldots, X_n\) sont mutuellement indépendantes si et seulement si : \[P(X_1 = x_1, \ldots, X_n = x_n) = P(X_1 = x_1) \times \ldots \times P(X_n = x_n)\]

Si \(X_1, \ldots, X_n\) sont mutuellement indépendantes, alors pour toute famille de fonctions réelles \(f_i\), on a : \((f_1(X_1), \ldots, f_n(X_n))\) sont indépendantes.

Soit \(X = (X_1, \ldots, X_n)^T\) un vecteur aléatoire. Dans le cas multidimensionnel, l’espérance scalaire est remplacée par un vecteur espérance. \[E(X) = (E(X_1), \ldots, E(X_n))^T\]

La variance unidimensionnelle est remplacée par la matrice symétrique de variance-covariance. Elle contient les variances en diagonale et les covariances ailleurs. On la note généralement \(\Sigma_X\). \[\Sigma_X = \begin{bmatrix} V(X_1) & \ldots & \text{Cov}(X_1, X_n) \\ \vdots & \ddots & \vdots \\ \text{Cov}(X_n, X_1) & \ldots & V(X_n) \end{bmatrix}\]

Notions de convergence

Si l’on pense à des données, vues comme réalisation de variables aléatoires \(X_1, \ldots, X_n\), il serait intéressant de se poser la question de savoir comment évolue cette suite lorsque \(n\) tend vers l’infini.

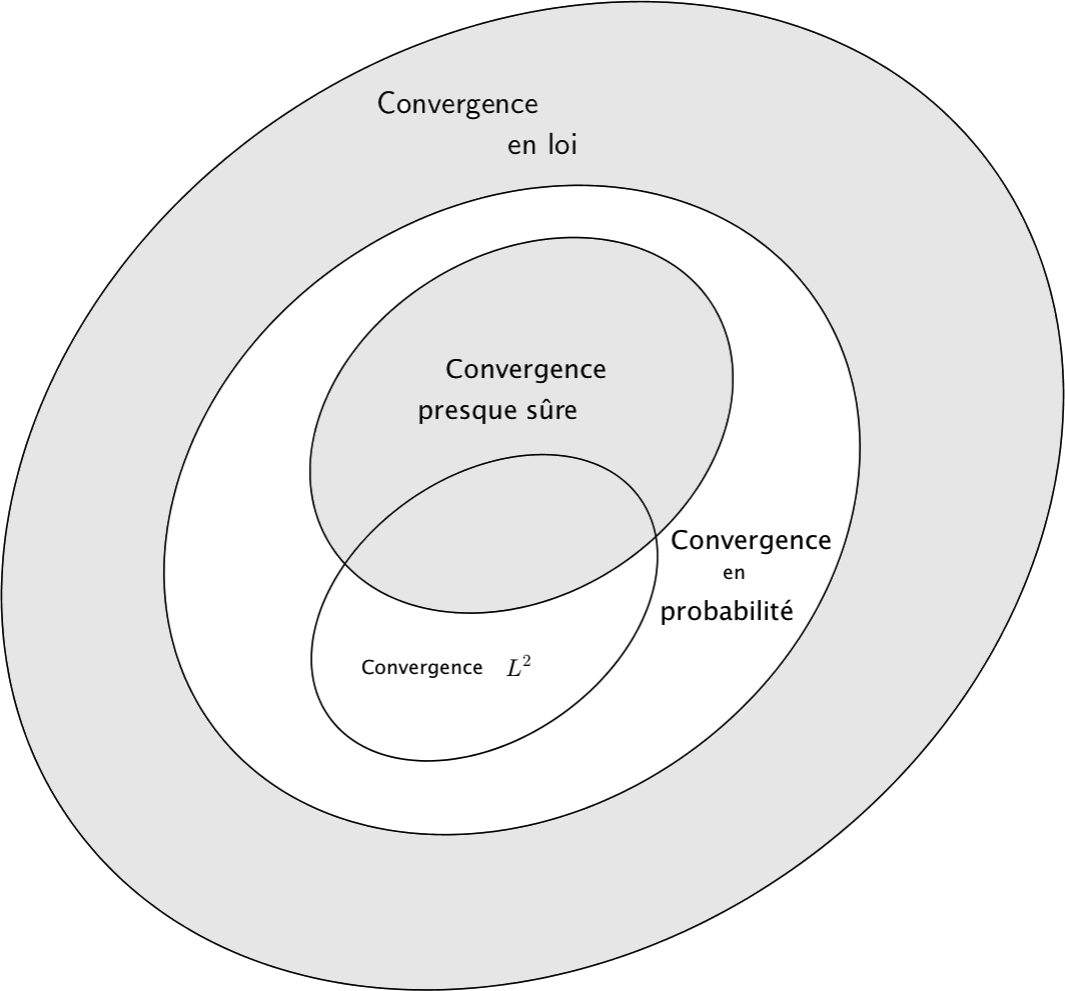
On dit que \((X_n)\) converge presque sûrement vers \(X\) et on note \(X_n \xrightarrow{\text{p.s.}} X\) si et seulement si : \(P\left(\lim_{{n\to+\infty}} X_n = X\right) = 1\)

On dit que \((X_n)\) converge en probabilité vers \(X\) et on note \(X_n \xrightarrow{\text{p}} X\) si et seulement si : \(\forall \varepsilon > 0, \quad P(|X_n - X| > \varepsilon) \rightarrow 0\)

On dit que \((X_n)\) converge en loi vers \(X\) et on note \(X_n \xrightarrow{\mathcal{L}} X\) si et seulement si : \(F_{X_n} \xrightarrow{n \to +\infty} F_X\) Où \(F_X\) dénote la fonction de répartition de \(X\).

On dit que \((X_n)\) converge en moyenne quadratique vers \(X\) et on note \(X_n \xrightarrow{m.q.} X\) si et seulement si : \(\mathbb{E}((X_n - X)^2) \rightarrow 0\) Cette définition peut se généraliser jusqu’à l’ordre \(n\), mais nous n’en aurons pas besoin.

Loi faible des grands nombres

Soit \(X_1, \ldots, X_n\) une suite de variables aléatoires indépendantes et de même loi telles que : \(\mathbb{E}(X_i) = \mu\) et \(\text{Var}(X_i) = \sigma^2\) alors :
\[\frac{1}{n} \sum_{i=1}^{n} X_i \xrightarrow{p} \mu \]

Loi forte des grands nombres

Soit \(X_1, \ldots, X_n\) une suite de variables aléatoires indépendantes et de même loi telles que : \(\mathbb{E}(X_i) = \mu\) et \(\text{Var}(X_i) = \sigma^2\), alors :
\[\frac{1}{n} \sum_{i=1}^{n} X_i \xrightarrow{p.s.} \mu\]

Théorème Central Limite

Soit \(X_1, \ldots, X_n\) une suite de variables aléatoires indépendantes et de même loi telles que : \(\mathbb{E}(X_i) = \mu\) et \(\text{Var}(X_i) = \sigma^2\), alors : \[\sqrt{n}\frac{\overline{X}_n - \mu}{\sigma} \xrightarrow{\mathcal{Loi}} \mathcal{N}(0, 1)\]

Statistique inférentielle : niveau basique

Echantillon / Estimateur

Le point de départ est un vecteur (ou un tableau dans le cas multidimensionnel) de données. Ces données peuvent être vues comme les réalisations \((x_1, x_2, \ldots, x_n)\) d’une variable aléatoire \(X\) qui dépend d’un certain paramètre \(\theta\) que nous allons chercher à estimer. Pour ce faire, nous allons construire un échantillon de cette variable. Un échantillon \((X_1, X_2, \ldots, X_n)\) est un n-uplet de variables aléatoires indépendantes qui suivent toutes la même loi (celle de \(X\)). Un estimateur de \(\theta\) est une fonction \(\hat{\theta} = f(X_1, X_2, \ldots, X_n)\) de notre échantillon, qui possède une loi de probabilité. Lorsque l’aléa est réalisé, \(\hat{\theta}(\omega) = f(x_1, x_2, \ldots, x_n)\) est une estimation de \(\theta\). Le but de ce cours est de construire le meilleur estimateur possible de \(\theta\).

Estimateur sans biais

Pour que l’estimation soit bonne, il faut que \(\hat{\theta}\) soit proche de \(\theta\). Comme \(\hat{\theta} = f(X_1, X_2, \ldots, X_n)\) est une variable aléatoire, on ne peut imposer de condition qu’à sa valeur moyenne.

On définit ainsi le biais : \[b_n(\hat{\theta}, \theta) = \mathbb{E}(\hat{\theta}_n) - \theta\]

Un estimateur est dit sans biais si \(b_n(\hat{\theta}, \theta) = 0\), c’est-à-dire : \[\mathbb{E}(\hat{\theta}_n) = \theta\]

Estimateur convergent

Un estimateur est dit convergent s’il converge en probabilité vers le paramètre à estimer : \[\hat{\theta}_n \xrightarrow{P} \theta\]

En pratique, tout estimateur sans biais et dont la variance tend vers 0 est convergent.

Estimateur optimal

La qualité d’un estimateur est mesurée à travers son erreur quadratique moyenne définie par : \[EQM(\hat{\theta}_n) = (b_n(\hat{\theta}, \theta))^2 + V(\hat{\theta}_n)\] Comme nous cherchons tout le temps (presque) des estimateurs sans biais, il reste à comparer les variances.

Un estimateur 𝜃̂1 est meilleur que 𝜃̂2 si : \[V(\hat{\theta}_1) < V(\hat{\theta}_2)\]

On définit la quantité d’information apportée par l’estimateur par : \[ I(\hat{\theta}_n) = -\left( \mathbb{E} \left( \frac{\partial L}{\partial \theta} \right) \right)^2 \] Où 𝐿(𝑥, 𝜃) = ∏ 𝑓(𝑥𝑖) (nous reviendrons sur sa définition)

L’inégalité de Rao-Cramer postule que la variance d’un estimateur ne peut pas aller en delà d’un certain seuil : \[V(\hat{\theta}_n) \geq \frac{1}{I(\hat{\theta}_n)}\] Un estimateur est optimal (ou efficace) si sa variance vérifie le cas d’égalité.

Construction d’un estimateur

La méthode du maximum de vraisemblance consiste à affecter \(𝜃\) la valeur qui maximise la probabilité d’observer \((𝑥_1, 𝑥_2, … , 𝑥_𝑛)\) lorsque l’aléa du vecteur \((𝑋_1, 𝑋_2, … , 𝑋_𝑛)\) tombe. Sans trop rentrer dans la théorie de la vraisemblance, nous allons présenter un algorithme en cinq étapes pour calculer cet estimateur (qui présente des propriétés assez séduisantes) :

Dans le cas continu : \[L(\mathbf{x}, \theta) = \prod_{i=1}^{n} f(x_i)\]

Dans le cas discret : \[L(\mathbf{x}, \theta) = \prod_{i=1}^{n} P(X_i = x_i)\]

Il s’agit de calculer un maximum, ce qui revient à dériver. Il s’agit ici d’un produit de n facteurs, ce qui rend la dérivation assez coriace. La fonction logarithmique présente des propriétés assez sympas pour faciliter cette tâche.

\[\frac{\partial (\ln(L))}{\partial \theta} = 0 \Rightarrow \theta = \theta_0\]

En s’assurant que : \[\frac{\partial^2 (\ln(L))}{\partial \theta^2} < 0\]

Comme le paramètre à estimer intervient dans la densité de probabilité, les moments théoriques sont souvent en fonction de ce paramètre. Ainsi, la méthode des moments consiste à égaliser les moments théoriques (espérance, variance) à leurs équivalents empiriques et à en dégager une estimation ponctuelle.

En pratique, il faut résoudre l’(les) équation(s) : \[\mathbb{E}(X) = \overline{X} \text{ et } \text{Var}(X) = S_n^2\] avec : \[\overline{X} = \frac{1}{n} \sum_{i=1}^{n} X_i \hspace{2cm} S_n^2 = \frac{1}{n} \sum_{i=1}^{n} (X_i - \overline{X})^2\]

Lorsqu’il s’agit de prendre une mesure 𝜃 avec un appareil doté d’une imprécision \(𝜀\), alors le problème d’estimation peut s’écrire : \(𝑋 = 𝜃 + 𝜀\). La méthode des moindres-carrés ordinaires consiste à trouver le paramètre \(𝜃\) qui minimise la somme des carrées des erreurs : \[𝜃_{𝑀𝐶𝑂} = \arg\min \left( \sum_{i=0}^n \varepsilon_i^2 \right) = \arg\min \left( \sum_{i=0}^n (X_i - \theta)^2 \right)\]

Intervalles de confiance

Un intervalle de confiance [\(A\), \(B\)] de niveau \(1 - \alpha\) est un intervalle aléatoire qui a la probabilité \(1 - \alpha\) de contenir le paramètre à estimer \(\theta\). Formellement, on écrit : \(P (t_1 (\theta) \leq f(X_1, \ldots, X_n) \leq t_2 (\theta)) = P(A \leq \theta \leq B) = 1 - \alpha\)

Test d’hypothèses

Dans le cadre d’un test d’hypothèse, nous cherchons à faire valoir une hypothèse en dépit d’une autre, qui lui est contradictoire.

On appellera la première (celle dont le rejet à tort sera le plus préjudiciable) « Hypothèse nulle » et la deuxième « Hypothèse alternative ».

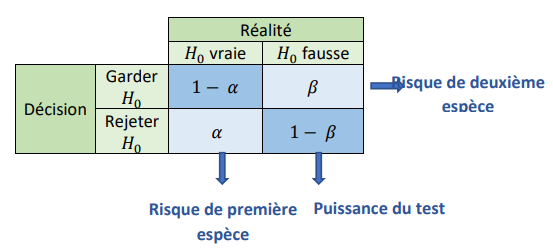
Les calculs qui se cachent derrière le choix de l’hypothèse à garder sont compliqués. Mais BONNE NOUVELLE, la machine fera tour à notre place. Il suffit juste de suivre correctement la méthode :

Construction d’intervalles de confiance

Les intervalles de confiance sont des outils essentiels en statistique pour estimer des paramètres inconnus tout en mesurant l’incertitude associée à cette estimation. Ci-dessous, vous trouverez un tableau présentant la construction des intervalles de confiance pour différents paramètres.

Economie

Définitions

Macroéconomie

La macroéconomie est l’étude économique d’un système ou de phénomènes à un niveau global de l’économie.

Microéconomie

La microéconomie se concentre sur l’observation et l’analyse des interactions à petite échelle.

Bien économique

“Chose utile à satisfaire un besoin, il faut que le bien soit disponible et en quantité limitée.

Un bien non économique est un bien qui s’obtient gratuitement, comme l’oxygène, contrairement à un bien économique qui s’obtient en payant.”

Agent économique

“Un agent économique est un individu ou un groupe d’individus constituant un centre de décision économique indépendant.”

Marché

“Le marché c’est une institution sociale qui permet l’échange entre l’offre et la demande.”

Asymétrie d’information

“L’asymétrie d’information concerne les situations où les agents d’un marché ne possèdent pas de la même information sur un produit que ce soit au sujet de ses qualités ou de ses défauts”

Concurrence Pure et Parfaite

La CPP repose sur cinq fondements :

• L’Atomicité du marché

Existence d’un grand nombre d’agent économique sur le marché, à tel un point que ni l’offre ni la demande ne peut exercer une action quelconque sur la production et les prix ;

• L’Homogénéité des produits

La préférence d’un produit à un autre du point de vue de l’acheteur se fait uniquement selon son prix ;

• Libre entrée et sortie sur le marché

Aucune firme ne peut s’opposer à l’arrivée d’un concurrent sur le marché, tout le monde est libre de l’intégrer ;

• Libre circulation des facteurs de production

Les facteurs de production (capital et travail) doivent être libre de se déplacer librement sans obstacle d’une industrie à l’autre ;

• La transparence de l’information

Offreurs et demandeurs sont parfaitement conscient des caractéristiques et prix des produits.

Monopole

“Le monopole est une situation dans un marché où un vendeur fait face aux multitudes vendeurs.”

Segmentation de marché

“La segmentation de marché est un découpage du marché en groupes homogènes selon des critères spécifiques, que ce soit des critères démographiques ou bien géo-graphiques.”

Discrimination par les prix

“La discrimination par les prix est le pouvoir de pratiquer des prix différents pour un même produit, peut s’appliquer sur la quantité ou bien selon la segmentation du marché.”

Utilité

“L’utilité mesure le bien-être liée à la consommation d’un bien.”

Actualisation

“L’Actualisation est un calcul permettant de transformer une valeur future en une valeur présente.”

Que vaut aujourd’hui les X euros que j’aurais demain ?

\[ V_a = \frac{V_f}{(1+i)^t} \]

\[ V_a : Valeur\ Actuelle \]

\[ V_f : Valeur\ future \] \[ i : Taux\ sans\ risque\\ \]

\[ t : Temps \]

Problèmes macroéconomiques

Il existe 4 grands problèmes macroéconomiques :

• Crises et récessions Ralentissement et/ou régression de l’activité économique ;

• Inflations Augmentation générale et durable du niveau des prix entraînant une perte du pouvoir d’achat de la monnaie ;

• Chômage Inactivité due au manque de travail ;

• Problème de l’équilibre extérieur Quand les importations sont plus importantes que les exportations, la balance commerciale est déséquilibrée.

La dissertation en économie

“On tient tout d’abord à remercier l’enseignant chercheur (en Philosophie économique, Théories économiques de la justice, Redistribution des revenus, Economie sociale, Economie publique), monsieur Jean-Sébastien Gharbi pour cette rubrique d’aide à la dissertation.”

On pense souvent que la dissertation en économie est un exercice difficile et qui récompense mal le travail. C’est totalement faux. La dissertation est un exercice dans lequel il est facile d’obtenir la moyenne, et même (avec un peu d’entraînement) d’obtenir systématiquement de très bonnes notes. C’est un exercice relativement facile parce que c’est un exercice en très grande partie formel : tout est une question de méthode.

Faire une dissertation, c’est montrer que vous êtes capable d’utiliser et de réorganiser vos connaissances pour répondre à une question de manière argumentée (c’est-à-dire sous la forme d’un raisonnement). Autrement dit :

• Une dissertation n’est pas une question de cours.

La première chose à faire, c’est de différencier question de cours et dissertation (qui sont souvent confondues). Une question de cours demande simplement de réciter un cours. Si vous ne faites que réciter votre cours dans un exercice de dissertation, vous aurez une mauvaise note. Pourquoi ? Parce que l’exercice de dissertation suppose de montrer que vous êtes capable d’utiliser et de réorganiser vos connaissances (dans un temps limité) – pas seulement de réciter une leçon apprise plus ou moins par cœur. Comme la question de cours, la dissertation suppose donc que vous savez des choses sur le sujet, mais il est important de comprendre que la dissertation porte tout autant sur votre aptitude à organiser vos idées que sur vos connaissances.

• Dans une dissertation, la réponse donnée n’est pas importante !

Une dissertation consiste toujours à répondre à une question. Les étudiants pensent parfois qu’il y a une « bonne » réponse à la question posée – qu’il s’agirait de trouver. D’ailleurs, cela contribue à l’idée (fausse) que la dissertation est un exercice aléatoire : si vous ne trouvez pas la bonne réponse, vous avez perdu. Cela aussi est faux : il n’y a (en général) pas de « bonne » réponse à la question posée par la dissertation. L’exercice de dissertation vient de la philosophie. Pensez-vous sérieusement que l’on puisse demander à un étudiant (ou à un professeur, d’ailleurs) de régler de façon définitive un débat philosophique qui a donné lieu à des controverses pendant des siècles en trois, quatre ou même sept heures ? La réponse évidente est « non ».

• Dans une dissertation, le plus important c’est l’argumentation !

Si on ne s’intéresse pas à la réponse donnée. C’est tout simplement, parce que ce qui intéresse votre lecteur, c’est la manière dont vous répondez : votre aptitude à utiliser vos connaissances de manière argumentative pour défendre une conclusion. Sur le principe, il serait donc possible de défendre une conclusion choquante ou même offensante dans une dissertation, pour la bonne raison qu’on n’évalue pas la réponse que vous donnez, mais la manière dont vous amenez votre réponse. Votre réponse, à la limite, on ne s’y intéresse pas. Une fois cela dit, il est assez évident qu’il est beaucoup plus facile de défendre une position modérée et consensuelle, qu’une position offensante pour de nombreuses personnes. C’est la raison pour laquelle, il n’est pas du tout conseillé de chercher la provocation gratuite dans une dissertation.

Comment on fait une dissertation ?

Analyse du sujet

L’analyse du sujet est la première étape de la dissertation et l’une des plus importantes. Une dissertation se présente sous la forme d’un sujet. Il faut isoler la ou les deux notions principales du sujet.

Il y a quatre grands types de sujets : les sujets ne contenant qu’une seule notion (ex : « Les discriminations en France »), les couples de notions (ex : « Capitalisme et démocratie »), les citations (ex : « Le système de production capitaliste est une démocratie économique dans laquelle chaque sou donne un droit de vote. Les consommateurs constituent le peuple souverain », Ludwig von Mises) ou une question (ex : « La croissance économique s’oppose-t-elle à la préservation de l’environnement ? »).

Dans tous les cas, l’objectif est d’arriver à une question (donc les sujets les plus simples à traiter à ce stade, ce sont les questions : ils vous donnent immédiatement le problème à traiter). Mais la première chose à faire (même quand on a déjà la question), c’est de trouver le couple de notions impliquées dans le sujet. Souvent, c’est absolument évident, mais parfois il faut un peu chercher.

Il faut éviter à tout prix de faire un exposé quand on attend de vous une dissertation. Un hors-sujet, c’est de ne pas traiter le bon sujet. Si vous répondez de manière factuelle à un sujet de dissertation, vous faites pire : vous faites un hors-exercice.

Recherche des idées

Une fois qu’on a identifié un couple de notions, il faut (au brouillon) essayer de faire la liste des éléments du cours qui relient les deux notions. Il est important de ne noter que les éléments qui relient les deux notions (pour ne pas risquer de se perdre dans des éléments qui concernent seulement une seule des deux notions). Sur chacune des notions que vous aurez à traiter en dissertation, on a écrit des livres entiers. Il est impossible de tout dire dessus dans une dissertation. On se limite donc à ce qui relie les deux notions de notre sujet. Évidemment, si un élément pertinent vous vient en tête et qu’il ne se trouve pas dans votre cours, n’hésitez pas à le noter. Si cet élément peut être utilisé dans votre raisonnement, même comme exemple, ce sera un plus indiscutable.

Dans un premier temps, on note tout ce qui se présente à l’esprit. Ce n’est que dans un deuxième temps, quand on a un certain nombre d’éléments que l’on se pose la question : « Est-ce qu’il y a une manière qui saute aux yeux de relier tous ces éléments en répondant à la question (si elle a été posée de manière directe) ou pour répondre à une question comprenant le couple de notions (si la question n’a pas été formulée dans le sujet) ? ». Si la réponse est positive, on a trouvé la question qui structurera notre devoir. Si ce n’est pas le cas, il faut essayer de trouver une question qui relie le plus grand nombre des éléments que l’on a noté sur son brouillon – et donc laisser de côté les éléments qui ne servent pas. Il arrive souvent qu’une partie des éléments que l’on note sur son brouillon ne soit pas utilisée dans le devoir. Bref, si notre sujet est un couple de notions ou une citation, il faut que l’on arrive à une question. Évidemment, quand notre sujet est déjà une question, on n’a pas autant de marge de manœuvre, mais en vérité, si on vous pose une question précise, c’est que vous avez les éléments pour y répondre dans le cours (donc la différence n’est pas très importante).

Mise en évidence d’un problème

Puisqu’elle ne doit pas être une question de fait, la question qui relie le plus d’éléments possibles parmi ceux qui associent les deux notions dans votre cours doit être une question conceptuelle. Pour le dire autrement, cette question doit être un problème (on parle souvent de « problématique » pour désigner ce problème dans le cadre d’une dissertation). Qu’est-ce qu’un problème ? C’est une question qui met en tension deux concepts et qui analyse les différents aspects de leur relation (conceptuelle).

Souvent les étudiants ont peur de ne pas trouver le « bon » problème. Pourtant, si on suit la méthode de dissertation, il n’y a pas de risque de se tromper. En effet, on ne doit pas choisir un problème d’abord (sans savoir si on a de quoi le traiter) et le traiter ensuite. Vous aurez noté qu’on procède exactement dans le sens inverse : on voit à quelle question on peut répondre avec les éléments qu’on a sur son brouillon et on pose précisément la question à laquelle on sait qu’on peut répondre.

Construction du plan

Pour la même raison qu’au-dessus, la construction du plan ne doit pas être très difficile : il s’agit de rassembler les différents éléments qui permettent de répondre à la question (au problème que l’on va poser) de façon à y apporter une réponse.

On va apporter la réponse que les éléments disponibles nous permettent d’atteindre. Il y a une seule contrainte : votre plan doit être suffisamment détaillé. Comme l’objectif de la dissertation, c’est de montrer que vous êtes capable d’utiliser et de réorganiser vos connaissances. Si vous ne faites que deux parties sans sous-parties à l’intérieur (il n’y aurait donc qu’une seule articulation logique), on trouvera que vous n’avez pas assez structuré votre devoir. Le découpage minimal, c’est d’avoir quatre éléments (en général, on fait deux grandes parties avec deux sous-parties chacune, donc on a trois articulations).

Vos parties et vos sous-parties doivent correspondre à des étapes de votre raisonnement (on dit souvent qu’il faut une idée par sous-partie), donc votre plan doit donner la structure du raisonnement grâce auquel vous allez répondre à la question posée. Le plan (qui est annoncé à la fin de l’introduction et qui doit être apparent dans le devoir, nous reviendrons sur ce point un peu plus loin) doit permettre de comprendre la structure de votre devoir d’un coup d’œil – simplement en lisant les titres.

Un élément qui permet de savoir si votre plan est bon, c’est de se demander si à la fin de la première partie, on est arrivé à un état de la réflexion différent de celui de la fin de l’introduction.

Qu’est-ce que la première partie a permis de comprendre ? Et est-ce que la seconde partie apporte quelque chose d’autre ? Si chaque partie représente une étape dans un raisonnement et que votre devoir complet est donc un raisonnement, votre plan est forcément bon : vu que c’est précisément ce qu’on attend de vous.

Il ne faut jamais faire deux sous-parties dans une partie sous la forme d’une seule phrase coupée par des points de suspension (ex : « A) L’organisation scientifique du travail a permis la croissance des trente glorieuses… », « B) mais, elle a aussi eu des conséquences négatives, notamment sur le plan social »). En effet, cela revient à pointer du doigt que vous opérez une coupure arbitraire (donc que vous n’articulez pas de manière assez nette les différentes parties de votre devoir). Sur le principe, les deux sous-parties sont reliées par les points de suspension et donc ne forment qu’une partie sans coupure. Préférez toujours les titres qui se succèdent sans être grammaticalement liés les uns aux autres. Dans l’exemple ci-dessus, il suffit de faire deux phrases pour découper les deux idées. Si on ne peut pas couper grammaticalement les deux titres, c’est la preuve que l’articulation pose problème.

Dans l’idéal, un plan est équilibré : chaque partie comprend le même nombre de sous-parties que l’autre et elles font à peu près la même longueur. Et si vous faites plus de sous-parties dans une partie que dans l’autre, il faut que les sous-parties soient un peu plus longues dans la partie qui contient moins de sous-parties. Remarquez que si vous faites un plan avec deux parties, deux sous-parties, ce dernier problème ne se pose pas.

Un point important et souvent totalement négligé par les étudiants : même quand c’est tentant, on ne fait jamais de plan centré sur les auteurs. Un plan par auteurs conduit très souvent à suivre l’ordre chronologique et à présenter les positions des auteurs sans les confronter réellement les unes aux autres . Ce qui doit structurer le plan, ce sont les concepts (c’est-à-dire les notions qui nous avaient permis de construire le problème à résoudre).

En réalité, il n’est pas rare qu’on suive plus ou moins l’ordre chronologie, mais il est essentiel de se focaliser sur les concepts, et pas sur les auteurs. Pourquoi ? Parce que l’enchaînement ou l’opposition de concepts constitue un raisonnement (ce que vous devez faire !), alors que l’enchaînement ou l’opposition d’auteurs constitue un exposé (ce que vous ne devez pas faire !). En réalité, c’est assez facile à faire il suffit de s’interdire de mentionner le nom des auteurs dans les titres de partie ou de sous-partie.

Vu que l’objectif du plan, c’est de répondre à une question qui met les deux notions du sujet en relation, les parties (ou les sous-parties) qui se focalisent sur une seule des deux notions sont à éviter à tout prix : elles sont simplement hors-sujet. Sur un sujet comme « capitalisme et démocratie », le plan « première partie : capitalisme », « deuxième partie : démocratie » est parmi les pires possibles.

Jusqu’à présent, nous n’avons encore rien écrit sur la copie elle-même. Nous n’avons travaillé que sur le brouillon. Nous avons deux notions clés, un problème et un plan. Ce sont les éléments fondamentaux du devoir. Il faut à présent passer à la rédaction. Nous allons nous intéresser d’abord à l’introduction.

La rédaction

(Introduction, Conclusion, Développement)

L’introduction est la partie la plus importante de la dissertation. Elle permet de savoir pourquoi le problème se pose, comment il se pose et comment il va être résolu. A quoi sert l’introduction ?

Le rôle de l’introduction, sa raison d’être, c’est de construire et d’énoncer le problème (la problématique) auquel le reste du devoir va répondre. Il ne suffit donc pas de poser la question (pour cela deux lignes suffiraient) et de commencer le développement. L’introduction, comme son nom le dit très bien, va introduire le problème, c’est-à-dire qu’elle va nous y amener, rapidement, certes, mais en plusieurs étapes très codifiées.

Une introduction de dissertation comprend obligatoirement (au minimum) cinq éléments : une accroche, une définition des termes du sujets, la construction du problème, l’énoncé du problème et l’annonce du plan. Comme une introduction de dissertation fait entre 20 lignes et une page et demie (grand maximum), il faut être efficace.

• L’accroche

Une introduction de dissertation suit des règles assez rigides. Elle commence toujours par une accroche.

Une « accroche », c’est une phrase ou deux qui vont contenir la ou les deux notion(s) du sujet. Son rôle est d’amener par étapes le lecteur vers la question que vous allez poser. Elle sert donc d’introduction à l’introduction. Une accroche peut être une citation (il y en a toujours dans un cours) ou un fait récent (le chômage a-t-il baissé récemment ? Un candidat à l’élection présidentielle a-t-il dit qu’il fallait juger sa politique en fonction de son impact sur le niveau de chômage ?). Si on n’a pas de citation ou de fait relevant de l’actualité, on peut amener le sujet de façon plus habituelle.

Il est important d’éviter un certain nombre de formules toutes faites et souvent utilisées comme « De tous temps... », « De tous temps, les hommes... » ou encore les affirmations très générales (et que vous ne justifierez pas) comme : « Le chômage est un phénomène économique important, c’est pourquoi il faut l’étudier ». Le défaut de tous ces débuts d’accroche, c’est qu’ils peuvent servir pour n’importe quel sujet et que cela se voit.

On met une accroche parce que cela permet de mentionner les termes du sujet sans commencer directement par une définition – ce qui constitue l’étape suivante.

• Définition des termes du sujet

L’accroche a introduit les notions, mais sans les définir – comme si tout le monde savait précisément de quoi il s’agit (ce qui n’est pas si surprenant, on ne passe pas son temps à définir tous les mots qu’on utilise). Mais, pour utiliser les deux notions du sujet de façon un peu plus précise, il faut les définir. Les définitions que l’on va donner dans une introduction n’ont pas pour objectif de définir les notions de manière exhaustive ou dans l’absolu. Elles doivent permettre de comprendre le lien (ou l’opposition) entre les deux notions et orienter l’introduction de façon à ce que l’on puisse construire le problème – avant de l’énoncer (autrement dit, elles doivent ouvrir la voie aux deux étapes suivantes de l’introduction).

Du coup, les définitions que l’on va donner vont dépendre du problème que l’on souhaite atteindre.

• Construction du problème

Comme on sait à quelle question on doit arriver (que cette question nous ait été donnée par le sujet ou que ce soit la question à laquelle on est le mieux armé pour apporter une réponse), il ne va pas être difficile de passer des définitions au problème. Cela suppose juste de montrer qu’avec les définitions que l’on vient de donner, il y a une question se pose avec force.

Encore une fois, cela peut sembler très artificiel (et ça l’est). Toutefois, l’intérêt de cet aspect artificiel, c’est qu’il nous garantit que l’on ne va pas se perdre en chemin. Quand on fait une dissertation, on ne cherche pas son chemin : on sait où on va et on ne fait qu’expliquer pourquoi on y va. Le sujet que l’on construit ne tombe pas du ciel, il vient de notre cours. Les définitions ne tombent pas du ciel, elles donnent les éléments qui vont nous permettre de poser la question à laquelle on sait déjà comment on va répondre. Bref, l’étape de construction du problème est importante parce qu’elle montre que vous avez des aptitudes pour vous faire comprendre à l’écrit (et il ne faut surtout pas la négliger), mais elle n’est pas une étape difficile ou magique.

Vous pourriez être surpris que l’on construise le sujet, alors qu’il nous est parfois donné sous forme de question (dans les autres cas, on comprend mieux pourquoi il est nécessaire de construire le problème). En fait, c’est une manière de montrer que vous êtes capable de vous approprier le sujet. Vous ne traitez pas le sujet parce qu’on vous l’a donné (même si vous c’est une des raisons pour lesquelles vous faites une dissertation), mais parce que vous comprenez pourquoi la question se pose. Et comment mieux montrer qu’on comprend un problème qu’en montrant en quoi il est problématique ? Autrement dit, même quand votre sujet a la forme d’une question, vous devez passer par l’étape de construction du sujet dans l’introduction.

• Enoncé du problème

L’énoncé du problème doit prendre la forme d’une question. Il est le point final de l’étape juste précédente. Une fois qu’on a les éléments qui permettent de comprendre que le problème se pose, il faut explicitement exprimer le problème lui-même. On exprime toujours le problème sous la forme d’une question (parce que c’est une manière de montrer qu’il appelle une réponse) et d’une question unique. Poser deux, trois ou quatre questions ce serait soit redire plusieurs fois la même chose (et si votre première question est claire, c’est inutile), soit poser (volontairement ou pas) plusieurs questions différentes. Or, vous ne pourrez pas répondre convenablement et dans les règles de la dissertation à plusieurs questions en un seul devoir. Vous devrez donc choisir entre ne pas traiter certaines des questions que vous avez explicitement posées (et dans ce cas pourquoi les poser explicitement) ou essayer de les traiter toutes (ce qui vous conduira à un devoir dont la ligne directrice sera au mieux difficile à suivre, au pire inexistante). Si on se rappelle du côté formel et rhétorique d’une dissertation, on comprend qu’il ne faut poser qu’une seule question : celle à laquelle vous apportez une réponse.

Lorsque le sujet est une question, faut-il répéter mot pour mot le sujet comme énoncé du problème ? Il y a deux écoles : la première dit qu’il faut reformuler la question pour montrer que vous la comprenez. Ainsi un sujet comme « Les dépenses publiques permettent-elles de réduire le chômage ? », on pourrait proposer une problématique comme « les dépenses publiques sont-elles efficaces à court et à long terme pour lutter contre le chômage ? ».

Si vous faites correctement votre travail de définition des termes et de construction du sujet (dans les deux étapes précédentes), je pense qu’aucun correcteur ne vous reprochera de reprendre le sujet mot pour mot dans votre énoncé du problème. Ce qui pose problème pour les partisans de la première façon de faire, c’est quand on peut se demander si l’étudiant comprend que la question qu’il pose est un problème conceptuel, c’est-à-dire qui vient d’une tension entre deux notions. Dans une introduction qui remplit correctement son rôle de construction du problème, le fait de répéter le sujet mot pour mot n’est pas un souci.

• Annonce du plan

Une introduction doit toujours se terminer par une annonce du plan (ce n’est pas une option, c’est une obligation). L’annonce de plan dit à votre lecteur comment vous allez répondre au problème que vous venez de poser. Dans une dissertation, on ne joue pas sur le suspens. On ne cherche pas à surprendre son correcteur. Il faut donc annoncer le plan de manière à ce qu’il comprenne que vous allez répondre au problème posé par un raisonnement et qu’il comprenne aussi quels vont être les principales étapes de votre raisonnement (c’est-à-dire de votre devoir).

Vous allez donc annoncer vos (deux ou trois) grandes parties. Il est conseillé fortement d’utiliser les formules (un peu lourdes en termes de style, mais très claires) « dans une première partie, nous montrerons que... », puis « dans une deuxième partie, nous verrons que ... ». Quand vous ne le faites pas, il arrive trop souvent que votre lecteur ne sache pas si vous allez faire formellement deux ou trois parties – pour peu que vous utilisiez des mots comme « et », « puis » ou « ensuite », qui peuvent aussi bien marquer des étapes à l’intérieur d’une grande partie que le passage d’une partie à une autre.

La conclusion

Vous pourriez être surpris de voir la conclusion arriver aussi tôt dans le devoir. La raison, c’est qu’il est inconcevable de ne pas répondre à la question posée en introduction – si vous ne répondez pas le devoir n’aura, littéralement, servi à rien. Or, il est évident qu’en partiel, on est souvent pris par le temps. On rédige donc la conclusion juste après avoir rédigé l’introduction au brouillon (on la rédige aussi au brouillon, d’ailleurs). Comme ça si on est pris par le temps, on pourra recopier la conclusion déjà prête avant de rendre le devoir. S’il faut couper quelque chose en raison du temps limité de l’épreuve, il vaut mieux couper un bout du développement que rendre une dissertation sans conclusion.

La première phrase de votre conclusion doit apporter la réponse à la question que vous avez posée en introduction. Elle doit le faire de façon absolument claire et donc il est conseillé de reprendre exactement la question en la tournant en une phrase affirmative ou en une phrase négative selon votre réponse. Le rôle de la conclusion, c’est de répondre à la question. Il ne faut pas qu’on relise la conclusion en se demandant quelle était la réponse – et même en se demandant si une réponse a été donnée. Cela ne vous empêche pas de donner une réponse nuancée, mais il faut une réponse claire.

Une conclusion de dissertation ne résume pas le devoir (on vient de le lire, c’est tout à fait inutile). Une conclusion n’introduit jamais un élément qui n’a pas été abordé dans le devoir, mais qui aurait pu y être discuté. Si jamais votre correcteur n’a pas vu que vous avez oublié de parler de quelque chose d’important, vous n’allez tout de même pas lui dire qu’il manque quelque chose dans votre devoir (chacun son boulot). La dissertation est un exercice de rhétorique, votre objectif, c’est de convaincre votre lecteur : ce n’est pas à vous de dire qu’il manque quelque chose, même si vous le savez.

On conseille parfois de finir sa dissertation sur une ouverture. Une ouverture est un nouveau problème qui se pose une fois que vous avez répondu au problème de votre devoir. Cela revient à suggérer une autre dissertation possible une fois qu’on considère votre réponse comme acceptée. Trop souvent, les étudiants finissent leurs devoirs de manière particulièrement maladroite parce qu’ils ne comprennent pas ce qu’est une ouverture. Mon conseil est d’éviter de faire une ouverture, au moins au début : ce n’est pas une obligation et cela peut donner une très mauvaise impression finale.

La rédaction du devoir

Une fois tout cela fait, on prend sa copie (totalement vierge à ce moment) et on commence à écrire dessus : on recopie l’introduction, on rédige le développement directement sur la copie (on ne rédige jamais son développement sur le brouillon, cela prend beaucoup trop de temps à recopier). Le développement du devoir doit contenir des titres apparents pour les parties et les sous-parties. Cela signifie que le titre de votre grande partie est marqué dans votre copie (précédé d’un « I) ») et qu’il est isolé du texte et souligné. Bref, on doit pouvoir voir apparaître d’un coup d’œil votre plan en survolant votre copie du regard.

Comme dit juste au-dessus, si on manque de temps, on coupe une partie du développement et on recopie la conclusion qui se trouve sur le brouillon. Attention : si vous ne rédigez pas tout le développement, mettez tout de même le plan apparent pour les parties et sous-parties non développées. C’est précisément parce qu’on a une idée de ce que vous auriez écrit qu’il est possible (en cas de gros manque de temps) de ne pas rédiger tout le développement. Si vous ne détaillez pas votre plan, c’est la trame de votre raisonnement qui manque et c’est beaucoup plus ennuyeux. Si vous ne pouvez pas rédiger tout le développement, je vous conseille de mettre des éléments que vous auriez utilisé sous forme de liste de tirets (en plus des titres apparents qui sont obligatoires).